
【題目】已知函數f(x)=log3(ax+b)的圖象經過點A(2,1)和B(5,2),an=an+b(n∈N*).
(1)求{an};
(2)設數列{an}的前n項和為Sn,bn![]() ,求{bn}的前n項和Tn.
,求{bn}的前n項和Tn.
 提分百分百檢測卷系列答案
提分百分百檢測卷系列答案 寶貝計劃期末沖刺奪100分系列答案
寶貝計劃期末沖刺奪100分系列答案科目:高中數學 來源: 題型:
【題目】針對時下的“抖音熱”某校團委對“學生性別和喜歡抖音是否有關”作了一次調查,其中被調查的男女生人數相同,男生喜歡抖音的人數占男生人數的![]() ,女生喜歡抖音的人數占女生人數
,女生喜歡抖音的人數占女生人數![]() ,若有
,若有![]() 的把握認為是否喜歡抖音和性別有關則調查人數中男生可能有( )人
的把握認為是否喜歡抖音和性別有關則調查人數中男生可能有( )人
附表:
| 0.050 | 0.010 |
| 3.841 | 6.635 |
附:
A.20B.40C.60D.80
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為平行四邊形,點
為平行四邊形,點![]() 在面
在面![]() 內的射影為
內的射影為![]() ,
,![]() ,點
,點![]() 到平面
到平面![]() 的距離為
的距離為![]() ,且直線
,且直線![]() 與
與![]() 垂直.
垂直.
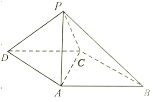
(Ⅰ)在棱![]() 上找一點
上找一點![]() ,使直線
,使直線![]() 與平面
與平面![]() 平行,并說明理由;
平行,并說明理由;
(Ⅱ)在(Ⅰ)的條件下,求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,曲線C1的參數方程為![]() (θ為參數),以原點為極點,x軸非負半軸為極軸,建立極坐標系,曲線C2的極坐標方程為
(θ為參數),以原點為極點,x軸非負半軸為極軸,建立極坐標系,曲線C2的極坐標方程為![]() .
.
(1)求曲線C1的極坐標方程以及曲線C2的直角坐標方程;
(2)若直線l:y=kx與曲線C1、曲線C2在第一象限交于P、Q,且|OQ|=|PQ|,點M的直角坐標為(1,0),求△PMQ的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,曲線C1的參數方程為![]() (θ為參數),以原點為極點,x軸非負半軸為極軸,建立極坐標系,曲線C2的極坐標方程為
(θ為參數),以原點為極點,x軸非負半軸為極軸,建立極坐標系,曲線C2的極坐標方程為![]() .
.
(1)求曲線C1的極坐標方程以及曲線C2的直角坐標方程;
(2)若直線l:y=kx與曲線C1、曲線C2在第一象限交于P、Q,且|OQ|=|PQ|,點M的直角坐標為(1,0),求△PMQ的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在正方體![]() 中,棱長為2,
中,棱長為2,![]() 分別為棱
分別為棱![]() 的中點,
的中點,![]() 為底面正方形
為底面正方形![]() 內一點(含邊界)且
內一點(含邊界)且![]() 與面
與面![]() 所成角的正切值為
所成角的正切值為![]() ,直線
,直線![]() 與面
與面![]() 的交點為
的交點為![]() ,當
,當![]() 到
到![]() 的距離最小時,則四面體
的距離最小時,則四面體![]() 外接球的表面積為___________.
外接球的表面積為___________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】十八大以來,黨中央提出要在2020年實現全面脫貧,為了實現這一目標,國家對“新農合”(新型農村合作醫療)推出了新政,各級財政提高了對“新農合”的補助標準.提高了各項報銷的比例,其中門診報銷比例如下:
表1:新農合門診報銷比例
醫院類別 | 村衛生室 | 鎮衛生院 | 二甲醫院 | 三甲醫院 |
門診報銷比例 | 60% | 40% | 30% | 20% |
根據以往的數據統計,李村一個結算年度門診就診人次情況如下:
表2:李村一個結算年度門診就診情況統計表
醫院類別 | 村衛生室 | 鎮衛生院 | 二甲醫院 | 三甲醫院 |
一個結算年度內各門診就診人次占李村總就診人次的比例 | 70% | 10% | 15% | 5% |
如果一個結算年度每人次到村衛生室、鎮衛生院、二甲醫院、三甲醫院門診平均費用分別為50元、100元、200元、500元.若李村一個結算年度內去門診就診人次為2000人次.
(Ⅰ)李村在這個結算年度內去三甲醫院門診就診的人次中,60歲以上的人次占了80%,從去三甲醫院門診就診的人次中任選2人次,恰好2人次都是60歲以上人次的概率是多少?
(Ⅱ)如果將李村這個結算年度內門診就診人次占全村總就診人次的比例視為概率,求李村這個結算年度每人次用于門診實付費用(報銷后個人應承擔部分)![]() 的分布列與期望.
的分布列與期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com