
 ax2+(1-a)x(a∈R且a≠0).
ax2+(1-a)x(a∈R且a≠0). ax2+(a-1)x
ax2+(a-1)x -ax+a-1=-
-ax+a-1=-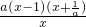 ,…(2分)
,…(2分) <1時,即a<-1時,令f′(x)>0,解得0<x<-
<1時,即a<-1時,令f′(x)>0,解得0<x<- 或x>1;
或x>1; <x<1.
<x<1. )和(1,+∞)上單調遞增,在(-
)和(1,+∞)上單調遞增,在(- ,1)上單調遞減…(4分)
,1)上單調遞減…(4分) =1時,即a=-1時,顯然,函數f(x)在(0,+∞)上單調遞增…(5分)
=1時,即a=-1時,顯然,函數f(x)在(0,+∞)上單調遞增…(5分) >1時,即-1<a<0時,令f′(x)>0,解得0<x<1或x>-
>1時,即-1<a<0時,令f′(x)>0,解得0<x<1或x>- ;
; .
. ,+∞)上單調遞增,(1,-
,+∞)上單調遞增,(1,- )上單調遞減…(6分)
)上單調遞減…(6分) )和(1,+∞)上單調遞增,在(-
)和(1,+∞)上單調遞增,在(- ,1)上單調遞減;
,1)上單調遞減; ,+∞)上單調遞增,(1,-
,+∞)上單調遞增,(1,- )上單調遞減…(7分)
)上單調遞減…(7分) a
a +(1-a)x1…①
+(1-a)x1…① a
a +(1-a)x2…②
+(1-a)x2…② a(x1+x2)+1-a](x1-x2)…③
a(x1+x2)+1-a](x1-x2)…③ =
= a(x1+x2)+1-a,
a(x1+x2)+1-a, =
= ,
, =
=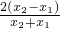 =
= ,
, =t,(t>1),上式化為:lnt=
=t,(t>1),上式化為:lnt=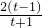 =2-
=2- ,…(11分)
,…(11分) =2…(12分)
=2…(12分) ,g′(t)=
,g′(t)= -
-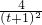 =
= ,
, =2成立.
=2成立. ax2+(a-1)x,f′(x)=-
ax2+(a-1)x,f′(x)=-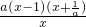 ,對a分a>0,a=0與a<0,三類討論,對a<0再根據1與-
,對a分a>0,a=0與a<0,三類討論,對a<0再根據1與- 的大小關系分三類討論即可求得答案;
的大小關系分三類討論即可求得答案; a(x1+x2)+1-a](x1-x2),假設C1在M處的切線與C2在N處的切線平線,則有
a(x1+x2)+1-a](x1-x2),假設C1在M處的切線與C2在N處的切線平線,則有 =
= a(x1+x2)+1-a,與前式聯立可得:
a(x1+x2)+1-a,與前式聯立可得: =
= ,設
,設 =t,(t>1),則lnt+
=t,(t>1),則lnt+ =2,構造函數g(t)=lnt+
=2,構造函數g(t)=lnt+ ,可判斷g(t)在(1,+∞)上遞增,g(t)>2恒成立.從而可證明C1在M處的切線與C2在N處的切線不平行.
,可判斷g(t)在(1,+∞)上遞增,g(t)>2恒成立.從而可證明C1在M處的切線與C2在N處的切線不平行.

科目:高中數學 來源: 題型:
| n |
 |
| i=1 |
| n |
 |
| i=1 |
| n |
 |
| i=1 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 | 2 |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
| 1 |
| 2 |
查看答案和解析>>
科目:高中數學 來源:2012-2013學年江西省新余四中高三(下)開學數學試卷(理科)(解析版) 題型:解答題
 ax2+(1-a)x(a∈R且a≠0).
ax2+(1-a)x(a∈R且a≠0).查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com