【題目】若關于x的不等式（m﹣1）x2﹣mx+m﹣1＞0的解集為空集，則實數m的取值為 ．
【答案】m≤ 
【解析】解：∵關于x的不等式（m﹣1）x2﹣mx+m﹣1＞0的解集為， ∴不等式（m﹣1）x2﹣mx+m﹣1≤0恒成立
①當m﹣1=0時，（m﹣1）x2﹣mx+m﹣1≤0，即x≥0，不是對任意x∈R恒成立；
②當m﹣1≠0時，x∈R，使（m﹣1）x2﹣mx+m﹣1≤0，
即m﹣1＜0且△=（﹣m）2﹣4（m﹣1）（m﹣1）≤0，
解得m≤
綜上，實數m的取值范圍是m≤ ．
所以答案是m≤ ．
【考點精析】解答此題的關鍵在于理解解一元二次不等式的相關知識，掌握求一元二次不等式
解集的步驟：一化：化二次項前的系數為正數;二判：判斷對應方程的根;三求：求對應方程的根;四畫：畫出對應函數的圖象;五解集：根據圖象寫出不等式的解集;規律：當二次項系數為正時，小于取中間，大于取兩邊．
新黃岡兵法密卷系列答案科目：高中數學 來源： 題型：
【題目】數列{an}的前n項和為Sn ， 若對于任意的正整數n都有Sn=2an﹣3n．
（1）設bn=an+3，求證：數列{bn}是等比數列，并求出{an}的通項公式；
（2）求數列{nan}的前n項和．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4-4：坐標系與參數方程
在平面直角坐標系
中，曲線
： 
，曲線
： 
（
為參數），以坐標原點
為極點， 
軸正半軸為極軸，建立極坐標系.
（Ⅰ）求曲線
， 
的極坐標方程；
（Ⅱ）曲線
： 
（
為參數， 
， 
）分別交
， 
于
， 
兩點，當
取何值時， 
取得最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示，在
中， 
的中點為
,且
，點
在
的延長線上，且
.固定邊
，在平面內移動頂點
，使得圓
與邊
，邊
的延長線相切，并始終與
的延長線相切于點
，記頂點
的軌跡為曲線
.以
所在直線為
軸， 
為坐標原點如圖所示建立平面直角坐標系.
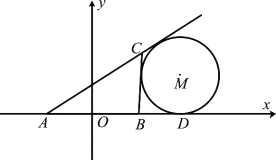
（Ⅰ）求曲線
的方程；
（Ⅱ）設動直線
交曲線
于
兩點，且以
為直徑的圓經過點
，求
面積的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知直線
，半徑為
的圓
與
相切，圓心在
軸上且在直線的上方．
（Ⅰ）求圓的標準方程；
（Ⅱ）過點
的直線與圓交于
兩點（
在軸上方），問在軸正半軸上是否存在點
，使得軸平分
？若存在，請求出點的坐標；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知： 
、 
、 
是同一平面上的三個向量，其中 =（1，2）．
（1）若| |=2 
，且 ∥ ，求 的坐標．
（2）若| |= 
，且 +2 與2 ﹣ 垂直，求 與 的夾角θ
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知a1=3，an=2an﹣1+（t+1）2n+3m+t（t，m∈R，n≥2，n∈N*）
（1）t=0，m=0時，求證： 
是等差數列；
（2）t=﹣1，m= 
是等比數列；
（3）t=0，m=1時，求數列{an}的通項公式和前n項和．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知空間四邊形ABCD的兩條對角線的長AC=6，BD=8，AC與BD所成的角為30o ， E，F，G，H分別是AB，BC，CD，DA的中點，求四邊形EFGH的面積．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com