
已知函數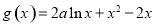 .
.
(1)當 時,討論函數
時,討論函數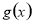 的單調性;
的單調性;
(2)當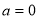 時,在函數
時,在函數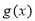 圖象上取不同兩點A、B,設線段AB的中點為
圖象上取不同兩點A、B,設線段AB的中點為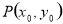 ,試探究函數
,試探究函數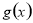 在Q
在Q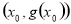 點處的切線與直線AB的位置關系?
點處的切線與直線AB的位置關系?
(3)試判斷當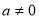 時
時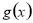 圖象是否存在不同的兩點A、B具有(2)問中所得出的結論.
圖象是否存在不同的兩點A、B具有(2)問中所得出的結論.
(1)函數 在定義域
在定義域 上單調遞增;(2)函數在Q點處的切線與直線AB平行;
上單調遞增;(2)函數在Q點處的切線與直線AB平行;
(3) 圖象不存在不同的兩點A、B具有(2)問中所得出的結論.
圖象不存在不同的兩點A、B具有(2)問中所得出的結論.
【解析】
試題分析:(1)求導即可知其單調性;(2)利用導數求出函數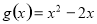 在點Q
在點Q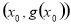 處的切線的斜率,再求出直線AB的斜率,可看出它們是相等的,所以函數在Q點處的切線與直線AB平行;
處的切線的斜率,再求出直線AB的斜率,可看出它們是相等的,所以函數在Q點處的切線與直線AB平行;
(3)設
 ,若
,若 滿足(2)中結論,則有
滿足(2)中結論,則有
 ,化簡得
,化簡得 (*).如果這個等式能夠成立,則存在,如果這個等式不能成立,則不存在.設
(*).如果這個等式能夠成立,則存在,如果這個等式不能成立,則不存在.設 ,則*式整理得
,則*式整理得 ,問題轉化成該方程在
,問題轉化成該方程在 上是否有解.再設函數
上是否有解.再設函數 ,下面通過導數即可知方程
,下面通過導數即可知方程 在
在 上是否有解,從而可確定函數
上是否有解,從而可確定函數 是否滿足(2)中結論.
是否滿足(2)中結論.
(1)由題知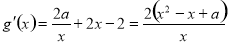 ,
,
因為 時,
時, ,函數
,函數 在定義域
在定義域 上單調遞增; 4分
上單調遞增; 4分
(2)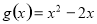 ,
, ,
,

所以函數Q點處的切線與直線AB平行; .7分
(3)設
 ,若
,若 滿足(2)中結論,有
滿足(2)中結論,有
 ,即
,即
即 (*) .9分
(*) .9分
設 ,則*式整理得
,則*式整理得 ,問題轉化成該方程在
,問題轉化成該方程在 上是否有解; 11分
上是否有解; 11分
設函數 ,則
,則 ,所以函數
,所以函數 在
在 單調遞增,即
單調遞增,即 ,即方程
,即方程 在
在 上無解,即函數
上無解,即函數 不滿足(2)中結論. 14分
不滿足(2)中結論. 14分
考點:導數的應用.


科目:高中數學 來源: 題型:
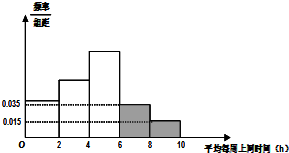 為了解高中生平均每周上網玩微信,刷微博,打游戲享受智能手機帶來的娛樂生活體驗,從高三年級學生中抽取部分同學進行調查,將所得的數據整理如下,畫出頻率分布直方圖(如圖),其中頻率分布直方圖從左至右前3個小組的頻率之比為1:3:5,第二組的頻數為150,則被調查的人數應為( )
為了解高中生平均每周上網玩微信,刷微博,打游戲享受智能手機帶來的娛樂生活體驗,從高三年級學生中抽取部分同學進行調查,將所得的數據整理如下,畫出頻率分布直方圖(如圖),其中頻率分布直方圖從左至右前3個小組的頻率之比為1:3:5,第二組的頻數為150,則被調查的人數應為( )| A、600 | B、400 |
| C、700 | D、500 |
查看答案和解析>>
科目:高中數學 來源:2013-2014學年四川省高三第六期3月階段性考試文科數學試卷(解析版) 題型:選擇題
已知函數 (
( ),則( )
),則( )
A. 必是偶函數 B.當
必是偶函數 B.當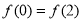 時,
時, 的圖象必須關于
的圖象必須關于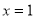 直線對稱;
直線對稱;
C. 有最大值
有最大值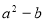 D. 若
D. 若 ,則
,則 在區間
在區間 上是增函數;
上是增函數;
查看答案和解析>>
科目:高中數學 來源:2013-2014學年四川省高三三診模擬理科數學試卷(解析版) 題型:選擇題
已知復數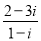 (
(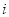 是虛數單位),它的實部與虛部的和是( )
是虛數單位),它的實部與虛部的和是( )
A.4 B.6 C.2 D.3
查看答案和解析>>
科目:高中數學 來源:2013-2014學年四川省高三三診模擬文科數學試卷(解析版) 題型:解答題
已知函數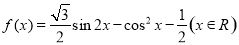
(1)當 時,求函數
時,求函數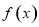 取得最大值和最小值;
取得最大值和最小值;
(2)設銳角 的內角A、B、C的對應邊分別是
的內角A、B、C的對應邊分別是 ,且
,且 ,若向量
,若向量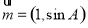 與向量
與向量 平行,求
平行,求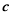 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com