
在平面直角坐標系 中,曲線
中,曲線 的參數方程為
的參數方程為 ,(其中
,(其中 為參數,
為參數, ),在極坐標系(以坐標原點
),在極坐標系(以坐標原點 為極點,以
為極點,以 軸非負半軸為極軸)中,曲線
軸非負半軸為極軸)中,曲線 的極坐標方程為
的極坐標方程為 .
.
(1)把曲線 和
和 的方程化為直角坐標方程;
的方程化為直角坐標方程;
(2)若曲線 上恰有三個點到曲線
上恰有三個點到曲線 的距離為
的距離為 ,求曲線
,求曲線 的直角坐標方程.
的直角坐標方程.
(1)曲線 的直角坐標方程為:
的直角坐標方程為: ;曲線
;曲線 的直角坐標方程為
的直角坐標方程為 ;
;
(2)曲線 的直角坐標方程為
的直角坐標方程為 .
.
解析試題分析:(1)對于曲線 ,把已知參數方程第一式和第二式移向,使等號右邊分別僅含
,把已知參數方程第一式和第二式移向,使等號右邊分別僅含 、
、 ,平方作和后可得曲線
,平方作和后可得曲線 的直角坐標方程;對于曲線
的直角坐標方程;對于曲線 ,把
,把 代入極坐標方程
代入極坐標方程 的展開式中即可得到曲線
的展開式中即可得到曲線 的直角坐標方程.
的直角坐標方程.
(2)由于圓 的半徑為
的半徑為 ,所以所求曲線
,所以所求曲線 與直線
與直線 平行,且與直線
平行,且與直線 相距
相距 時符合題意.利用兩平行直線的距離等于
時符合題意.利用兩平行直線的距離等于 ,即可求出
,即可求出 ,進而得到曲線
,進而得到曲線 的直角坐標方程.
的直角坐標方程.
試題解析:(1)曲線 的參數方程為
的參數方程為 ,即
,即 ,將兩式子平方化簡得,
,將兩式子平方化簡得,
曲線 的直角坐標方程為:
的直角坐標方程為: ;
;
曲線 的極坐標方程為
的極坐標方程為 ,即
,即 ,
,
所以曲線 的直角坐標方程為
的直角坐標方程為 .
.
(2)由于圓 的半徑為
的半徑為 ,故所求曲線
,故所求曲線 與直線
與直線 平行,且與直線
平行,且與直線 相距
相距 時符合題意.由
時符合題意.由 ,解得
,解得 .故曲線
.故曲線 的直角坐標方程為
的直角坐標方程為 .
.
考點:圓的參數方程;直線與圓的位置關系;簡單曲線的極坐標方程.


 口算心算速算應用題系列答案
口算心算速算應用題系列答案 同步拓展閱讀系列答案
同步拓展閱讀系列答案科目:高中數學 來源: 題型:解答題
已知圓 的方程為
的方程為 ,直線
,直線
 ,設點
,設點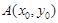 .
.
(1)若點 在圓
在圓 外,試判斷直線
外,試判斷直線 與圓
與圓 的位置關系;
的位置關系;
(2)若點 在圓
在圓 上,且
上,且 ,
, ,過點
,過點 作直線
作直線 分別交圓
分別交圓 于
于 兩點,且直線
兩點,且直線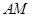 和
和 的斜率互為相反數;
的斜率互為相反數;
① 若直線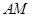 過點
過點 ,求
,求 的值;
的值;
② 試問:不論直線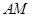 的斜率怎樣變化,直線
的斜率怎樣變化,直線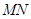 的斜率是否為定值?若是,求出該定值;若不是,說明理由.
的斜率是否為定值?若是,求出該定值;若不是,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知圓C過點P(1,1),且與圓M:(x+2)2+(y+2)2=r2(r>0)關于直線x+y+2=0對稱.
(1)求圓C的方程;
(2)過點P作兩條相異直線分別與圓C相交于A、B,且直線PA和直線PB的傾斜角互補,O為坐標原點,試判斷直線OP和AB是否平行?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
設直線3x+4y-5=0與圓C1:  交于A, B兩點, 若圓C2的圓心在線段AB上, 且圓C2與圓C1相切, 切點在圓C1的劣弧
交于A, B兩點, 若圓C2的圓心在線段AB上, 且圓C2與圓C1相切, 切點在圓C1的劣弧 上, 則圓C2的半徑的最大值是_______
上, 則圓C2的半徑的最大值是_______
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com