
已知數列{an}的前n項和Sn=2n+1-2,等差數列{bn}中,b2=a2,且bn+3+bn-1=2bn+4,(n 2,n
2,n N+),則bn=
N+),則bn=
| A.2n+2 | B.2n | C.n-2 | D.2n-2 |
科目:高中數學 來源: 題型:解答題
已知關于x的方程:x2-(6+i)x+9+ai=0(a∈R)有實數根b.
(1)求實數a,b的值.
(2)若復數滿足|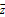 -a-bi|-2|z|=0,求z為何值時,|z|有最小值,并求出|z|的最小值.
-a-bi|-2|z|=0,求z為何值時,|z|有最小值,并求出|z|的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
設 為拋物線
為拋物線 (
( )的焦點,
)的焦點,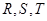 為該拋物線上三點,若
為該拋物線上三點,若 ,且
,且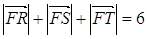
(Ⅰ)求拋物線 的方程;
的方程;
(Ⅱ) 點的坐標為(
點的坐標為(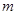 ,
, )其中
)其中 ,過點F作斜率為
,過點F作斜率為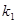 的直線與拋物線交于
的直線與拋物線交于 、
、 兩點,
兩點, 、
、 兩點的橫坐標均不為
兩點的橫坐標均不為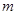 ,連結
,連結 、
、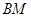 并延長交拋物線于
并延長交拋物線于 、
、 兩點,設直線
兩點,設直線 的斜率為
的斜率為 .若
.若 ,求
,求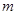 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:單選題
若在數列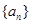 中,對任意正整數
中,對任意正整數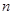 ,都有
,都有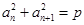 (常數),則稱數列
(常數),則稱數列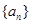 為“等方和數列”,稱
為“等方和數列”,稱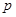 為“公方和”,若數列
為“公方和”,若數列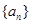 為“等方和數列”,其前
為“等方和數列”,其前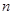 項和為
項和為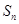 ,且“公方和”為
,且“公方和”為 ,首項
,首項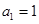 ,則
,則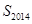 的最大值與最小值之和為( )
的最大值與最小值之和為( )
A. | B.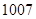 | C. | D.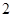 |
查看答案和解析>>
科目:高中數學 來源: 題型:單選題
兩千多年前,古希臘畢達哥拉斯學派的數學家曾經在沙灘上研究數學問題.他們在沙灘上畫點或用小石子表示數,按照點或小石子能排列的形狀對數進行分類.如下圖中實心點的個數 ,
, ,
, ,
, ,…為梯形數.根據圖形的構成,記此數列的第
,…為梯形數.根據圖形的構成,記此數列的第 項為
項為 ,則
,則 ( )
( )
A. | B. | C. | D. |
查看答案和解析>>
科目:高中數學 來源: 題型:單選題
若數列{an}滿足 -
- =d(n∈N*,d為常數),則稱數列{an}為“調和數列”.已知正項數列{
=d(n∈N*,d為常數),則稱數列{an}為“調和數列”.已知正項數列{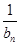 }為“調和數列”,且b1+b2+…+b9=90,則b4·b6的最大值是( )
}為“調和數列”,且b1+b2+…+b9=90,則b4·b6的最大值是( )
| A.10 | B.100 | C.200 | D.400 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com