
定義在R上的偶函數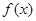 滿足
滿足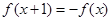 ,且在[-1,0]上單調遞增,
,且在[-1,0]上單調遞增,
設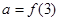 ,
,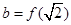 ,
,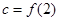 ,則
,則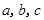 的大小關系是( )
的大小關系是( )
A. | B.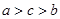  | C.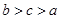  | D.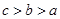 |
D
解析考點:函數單調性的性質;函數奇偶性的性質;函數的周期性.
專題:計算題.
分析:先根據條件推斷出函數為以2為周期的函數,根據f(x)是偶函數,在[-1,0]上單調遞增推斷出在[0,1]上是減函數.減函數,進而利用周期性使a=f(1),b=f(2- 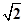 ),c=f(2)=f(0)進而利用自變量的大小求得函數的大小,則a,b,c的大小可知.
),c=f(2)=f(0)進而利用自變量的大小求得函數的大小,則a,b,c的大小可知.
解答:解:由條件f(x+1)=-f(x),可以得:
f(x+2)=f((x+1)+1)=-f(x+1)=f(x),所以f(x)是個周期函數.周期為2.
又因為f(x)是偶函數,所以圖象在[0,1]上是減函數.
a=f(3)=f(1+2)=f(1),
b=f(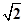 )=f(
)=f(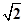 -2)=f(2-
-2)=f(2-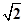 )
)
c=f(2)=f(0)
0<2-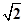 <1
<1
所以a<b<c
故選D
點評:本題主要考查了函數單調性,周期性和奇偶性的應用.考查了學生分析和推理的能力.


 科學實驗活動冊系列答案
科學實驗活動冊系列答案科目:高中數學 來源: 題型:單選題
已知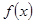 是R上的偶函數,且在區間
是R上的偶函數,且在區間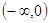 上是增函數,若
上是增函數,若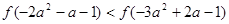 ,那么實數
,那么實數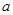 的取值范圍是( )
的取值范圍是( )
| A.(-1,0) | B.(-∞,0)∪(3,+∞) | C.(3,+∞) | D.(0,3) |
查看答案和解析>>
科目:高中數學 來源: 題型:單選題
給出下列三個函數圖像:

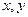 都有
都有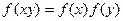 成立; ②對任意實數
成立; ②對任意實數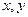 都有
都有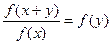 成立;
成立;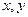 都有
都有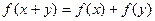 成立. 則下列對應關系最恰當的是
成立. 則下列對應關系最恰當的是 A. 和①, 和①,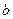 和②,c和③ 和②,c和③ | B.c和①,b和②, 和③ 和③ |
C.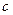 和①, 和①, 和②, 和②,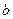 和③ 和③ | D.b和①,c和②, 和③ 和③ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com