
【題目】已知二次函數f(x)=ax2+bx+c.
(1)若f(﹣1)=0,f(0)=0,求出函數f(x)的零點;
(2)若f(x)同時滿足下列條件:①當x=﹣1時,函數f(x)有最小值0,②f(1)=1求函數f(x)的解析式;
(3)若f(1)≠f(3),證明方程f(x)= ![]() [f(1)+f(3)]必有一個實數根屬于區間(1,3)
[f(1)+f(3)]必有一個實數根屬于區間(1,3)
科目:高中數學 來源: 題型:
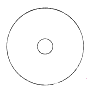
【題目】如圖,半徑為![]() 的圓形紙板內有一個相同圓心的半徑為
的圓形紙板內有一個相同圓心的半徑為![]() 的小圓,現將半徑為
的小圓,現將半徑為![]() 的一枚硬幣拋到此紙板上,使整塊硬幣完全隨機落在紙板內,則硬幣與小圓無公共點的概率為( )
的一枚硬幣拋到此紙板上,使整塊硬幣完全隨機落在紙板內,則硬幣與小圓無公共點的概率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在極坐標系中,點![]() ,曲線
,曲線 ![]() ,以極點為坐標原點,極軸為
,以極點為坐標原點,極軸為![]() 軸正半軸建立直角坐標系.
軸正半軸建立直角坐標系.
(1)在直角坐標系中,求點![]() 的直角坐標及曲線
的直角坐標及曲線![]() 的參數方程;
的參數方程;
(2)設點![]() 為曲線
為曲線![]() 上的動點,求
上的動點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2sin2( ![]() +x)﹣
+x)﹣ ![]() cos2x,
cos2x,
(1)求f(x)的最小正周期及單調遞減區間;
(2)當x ![]() 時,求f(x)的最大值和最小值.
時,求f(x)的最大值和最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知向量 ![]() =(sinx,cosx),
=(sinx,cosx), ![]() =(sin(x﹣
=(sin(x﹣ ![]() ),sinx),函數f(x)=2
),sinx),函數f(x)=2 ![]()
![]() ,g(x)=f(
,g(x)=f( ![]() ).
).
(1)求f(x)在[ ![]() ,π]上的最值,并求出相應的x的值;
,π]上的最值,并求出相應的x的值;
(2)計算g(1)+g(2)+g(3)+…+g(2014)的值;
(3)已知t∈R,討論g(x)在[t,t+2]上零點的個數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=Asin(ωx+φ),x∈R(其中 ![]() )的圖象與x軸的交點中,相鄰兩個交點之間的距離為
)的圖象與x軸的交點中,相鄰兩個交點之間的距離為 ![]() ,且圖象上一個最低點為
,且圖象上一個最低點為 ![]() .
.
(1)求f(x)的解析式;
(2)當 ![]() ,求f(x)的值域.
,求f(x)的值域.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com