
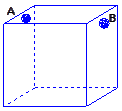
 為處理含有某種雜質的污水,要制造一個底寬為2米的無蓋長方體沉淀箱(如圖),污水從A孔流入,經沉淀后從B孔流出,設箱體的長度為a米,高度為b米,已知流出的水中該雜質的質量分數與a、b的乘積ab成反比,現有制箱材料60平方米,問當a、b各為多少米時,經沉淀后流出的水中該雜質的質量分數最小(A、B孔的面積忽略不計)?
為處理含有某種雜質的污水,要制造一個底寬為2米的無蓋長方體沉淀箱(如圖),污水從A孔流入,經沉淀后從B孔流出,設箱體的長度為a米,高度為b米,已知流出的水中該雜質的質量分數與a、b的乘積ab成反比,現有制箱材料60平方米,問當a、b各為多少米時,經沉淀后流出的水中該雜質的質量分數最小(A、B孔的面積忽略不計)?
當a=6,b=3時,經沉淀后流出的水中該雜質的質量分數最小.
解法一:設經沉淀后流出的水中該雜質的質量分數為y,則由條件y=![]() (k>0為比例系數)其中a、b滿足2a+4b+2ab=60 ①
(k>0為比例系數)其中a、b滿足2a+4b+2ab=60 ①
要求y的最小值,只須求ab的最大值.
由①(a+2)(b+1)=32(a>0,b>0)且ab=30–(a+2b)
應用重要不等式a+2b=(a+2)+(2b+2)–4≥![]()
∴ab≤18,當且僅當a=2b時等號成立
將a=2b代入①得a=6,b=3.
故當且僅當a=6,b=3時,經沉淀后流出的水中該雜質的質量分數最小.
解法二:由2a+4b+2ab=60,得![]() ,
,
記![]() (0<a<30)則要求y的最小值只須求u的最大值.
(0<a<30)則要求y的最小值只須求u的最大值.
由![]() ,令u′=0得a=6
,令u′=0得a=6
且當0<a<6時,u′>0,當6<u<30時u′<0,
∴![]() 在a=6時取最大值,此時b=3.
在a=6時取最大值,此時b=3.
從而當且僅當a=6,b=3時,y=![]() 取最小值.
取最小值.


科目:高中數學 來源: 題型:
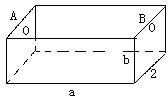 如圖,為處理含有某種雜質的污水,要制造一底寬為2米的無蓋長方體沉淀箱,污水從A孔流入,經沉淀后從B孔流出.設箱體的長度為a米,高度為b米.已知流出的水中該雜質的質量分數與a,b的乘積ab成反比.現有制箱材料60平方米.問當a,b各為多少米時,經沉淀后流出的水中該雜質的質量分數最小(A、B孔的面積忽略不計).
如圖,為處理含有某種雜質的污水,要制造一底寬為2米的無蓋長方體沉淀箱,污水從A孔流入,經沉淀后從B孔流出.設箱體的長度為a米,高度為b米.已知流出的水中該雜質的質量分數與a,b的乘積ab成反比.現有制箱材料60平方米.問當a,b各為多少米時,經沉淀后流出的水中該雜質的質量分數最小(A、B孔的面積忽略不計).查看答案和解析>>
科目:高中數學 來源: 題型:

查看答案和解析>>
科目:高中數學 來源: 題型:
如圖,為處理含有某種雜質的污水,要制造一底寬為2米的無蓋長方體沉淀箱,污水從![]() 孔流入,經沉淀后從
孔流入,經沉淀后從![]() 孔流出,設箱體的長為
孔流出,設箱體的長為![]() 米,高為
米,高為![]() 米.已知流出的水中該雜質的質量分數與
米.已知流出的水中該雜質的質量分數與![]() ,
,![]() 的乘積
的乘積![]() 成反比,現有制箱材料60平方米,問當
成反比,現有制箱材料60平方米,問當![]() ,
,![]() 各為多少米時,經沉淀后流出的水中該雜質的質量分數最小(
各為多少米時,經沉淀后流出的水中該雜質的質量分數最小(![]() ,
,![]() 孔的面積忽略不計).
孔的面積忽略不計).

查看答案和解析>>
科目:高中數學 來源: 題型:
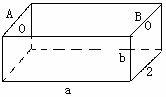
如圖,為處理含有某種雜質的污水,要制造一底寬為2米的無蓋長方體沉淀箱。污水從A孔流入,經沉淀后從B孔流出。設箱體的長度為a米,高度為b米。已知流出的水中該雜質的質量分數與a,b的乘積ab成反比。現有制箱材料60平方米。問當a,b各為多少米時,經沉淀后流出的水中該雜質的質量分數最小(A、B孔的面積忽略不計)。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com