
【題目】下列關(guān)于古典概型的說法中正確的是( )
①試驗中所有可能出現(xiàn)的基本事件只有有限個;
②每個事件出現(xiàn)的可能性相等;
③每個基本事件出現(xiàn)的可能性相等;
④基本事件的總數(shù)為n,隨機事件A若包含k個基本事件,則![]() .
.
A. ②④ B. ③④ C. ①④ D. ①③④
 千里馬走向假期期末仿真試卷寒假系列答案
千里馬走向假期期末仿真試卷寒假系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】在如圖所示的幾何體中,四邊形![]() 是等腰梯形,
是等腰梯形, ![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() .
.
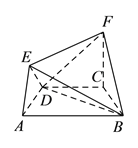
(![]() )求證:
)求證: ![]() 平面
平面![]() .
.
(![]() )求二面角
)求二面角![]() 的余弦值.
的余弦值.
(![]() )在線段
)在線段![]() (含端點)上,是否存在一點
(含端點)上,是否存在一點![]() ,使得
,使得![]() 平面
平面![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
【答案】(![]() )見解析;(
)見解析;(![]() )
)![]() ;(
;(![]() )存在,
)存在, ![]()
【解析】試題分析:(1)由題意,證明![]() ,
, ![]() ,證明
,證明![]() 面
面![]() ;(2)建立空間直角坐標(biāo)系,求平面
;(2)建立空間直角坐標(biāo)系,求平面![]() 和平面
和平面![]() 的法向量,解得余弦值為
的法向量,解得余弦值為![]() ;(3)得
;(3)得![]() ,
, 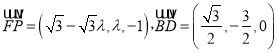 ,所以
,所以![]() ,
, ![]() ,所以存在
,所以存在![]() 為
為![]() 中點.
中點.
試題解析:
(![]() )∵
)∵![]() ,
, ![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
, ![]() .
.
∵![]() ,且
,且![]() ,
,
![]() 、
、![]() 面
面![]() ,∴
,∴![]() 面
面![]() .
.
(![]() )知
)知![]() ,∴
,∴![]() .
.
∵![]() 面
面![]() ,
, ![]() ,
, ![]() ,
, ![]() 兩兩垂直,以
兩兩垂直,以![]() 為坐標(biāo)原點,
為坐標(biāo)原點,
以![]() ,
, ![]() ,
, ![]() 為
為![]() ,
, ![]() ,
, ![]() 軸建系.
軸建系.
設(shè)![]() ,則
,則![]() ,
, ![]() ,
,  ,
, ![]() ,
, ![]() ,
,
∴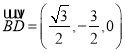 ,
, ![]() .
.
設(shè)![]() 的一個法向量為
的一個法向量為![]() ,
,
∴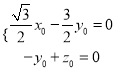 ,取
,取![]() ,則
,則![]() .
.
由于![]() 是面
是面![]() 的法向量,
的法向量,
則 .
.
∵二面角![]() 為銳二面角,∴余弦值為
為銳二面角,∴余弦值為![]() .
.
(![]() )存在點
)存在點![]() .
.
設(shè)![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
, ![]() .
.
∵![]() 面
面![]() ,
, 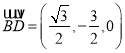 .
.
若![]() 面
面![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴![]() ,∴存在
,∴存在![]() 為
為![]() 中點.
中點.

【題型】解答題
【結(jié)束】
19
【題目】已知函數(shù)![]() .
.
(![]() )當(dāng)
)當(dāng)![]() 時,求此函數(shù)對應(yīng)的曲線在
時,求此函數(shù)對應(yīng)的曲線在![]() 處的切線方程.
處的切線方程.
(![]() )求函數(shù)
)求函數(shù)![]() 的單調(diào)區(qū)間.
的單調(diào)區(qū)間.
(![]() )對
)對![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() :
:![]() 經(jīng)過點
經(jīng)過點![]() ,離心率為
,離心率為![]() .
.
(1)求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)過坐標(biāo)原點![]() 作直線
作直線![]() 交橢圓
交橢圓![]() 于
于![]() 、
、![]() 兩點,過點
兩點,過點![]() 作
作![]() 的平行線交橢圓
的平行線交橢圓![]() 于
于![]() 、
、![]() 兩點.是否存在常數(shù)
兩點.是否存在常數(shù)![]() , 滿足
, 滿足![]() ?若存在,求出這個常數(shù);若不存在,請說明理由.
?若存在,求出這個常數(shù);若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() 為偶函數(shù),且當(dāng)
為偶函數(shù),且當(dāng)![]() 時,
時,![]() .記
.記![]() .給出下列關(guān)于函數(shù)
.給出下列關(guān)于函數(shù)![]() 的說法:①當(dāng)
的說法:①當(dāng)![]() 時,
時,![]() ;②函數(shù)
;②函數(shù)![]() 為奇函數(shù);③函數(shù)
為奇函數(shù);③函數(shù)![]() 在
在![]() 上為增函數(shù);④函數(shù)
上為增函數(shù);④函數(shù)![]() 的最小值為
的最小值為![]() ,無最大值.其中正確的是______.
,無最大值.其中正確的是______.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() ,且函數(shù)
,且函數(shù)![]() 是偶函數(shù).
是偶函數(shù).
(1)求![]() 的解析式;.
的解析式;.
(2)若不等式![]() 在
在![]() 上恒成立,求n的取值范圍;
上恒成立,求n的取值范圍;
(3)若函數(shù) 恰好有三個零點,求k的值及該函數(shù)的零點.
恰好有三個零點,求k的值及該函數(shù)的零點.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列說法正確的是( )
A.過![]() ,
,![]() 兩點的直線方程為
兩點的直線方程為![]()
B.點![]() 關(guān)于直線
關(guān)于直線![]() 的對稱點為
的對稱點為![]()
C.直線![]() 與兩坐標(biāo)軸圍成的三角形的面積是2
與兩坐標(biāo)軸圍成的三角形的面積是2
D.經(jīng)過點![]() 且在
且在![]() 軸和
軸和![]() 軸上截距都相等的直線方程為
軸上截距都相等的直線方程為![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知圓![]() 的一條直角是橢圓
的一條直角是橢圓![]() 的長軸,動直線
的長軸,動直線![]() ,當(dāng)
,當(dāng)![]() 過橢圓
過橢圓![]() 上一點
上一點![]() 且與圓
且與圓![]() 相交于點
相交于點![]() 時,弦
時,弦![]() 的最小值為
的最小值為![]() .
.
(1)求圓即橢圓![]() 的方程;
的方程;
(2)若直線![]() 是橢圓
是橢圓![]() 的一條切線,
的一條切線,![]() 是切線上兩個點,其橫坐標(biāo)分別為
是切線上兩個點,其橫坐標(biāo)分別為![]() ,那么以
,那么以![]() 為直徑的圓是否經(jīng)過
為直徑的圓是否經(jīng)過![]() 軸上的定點?如果存在,求出定點坐標(biāo);若不存在,請說明理由.
軸上的定點?如果存在,求出定點坐標(biāo);若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在發(fā)生某公共衛(wèi)生事件期間,有專業(yè)機構(gòu)認(rèn)為該事件在一段時間沒有發(fā)生在規(guī)模群體感染的標(biāo)志為“連續(xù)10天,每天新增疑似病例不超過7人”.根據(jù)過去10天甲、乙、丙、丁四地新增疑似病例數(shù)據(jù),一定符合該標(biāo)志的是
A. 甲地:總體均值為3,中位數(shù)為4 B. 乙地:總體均值為1,總體方差大于0
C. 丙地:中位數(shù)為2,眾數(shù)為3 D. 丁地:總體均值為2,總體方差為3
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com