【題目】如圖所示，在三棱錐P-ABC中，平面PAB⊥平面ABC，△ABC是邊長為
的等邊三角形，
，點O，M分別是AB，BC的中點.
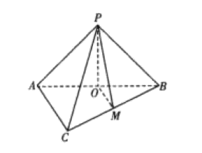
（1）證明：AC//平面POM；
（2）求點B到平面POM的距離.
【答案】（1）證明見解析；（2）
【解析】
（1）證明直線
平行平面POM內的直線
，再利用線面平行判定定理證明；
（2）作BN⊥OM，垂足為N，先證明BN⊥平面POM，得到線段BN的長即為點B到平面POM的距離，再從△BOM中求得BN的長.
（1）∵點O，M分別是AB，BC的中點，∴OM//AC.
又∵OM
平面POM，AC
平面POM，
∴AC//平面POM.
（2）如圖所示，作BN⊥OM，垂足為N，
∵
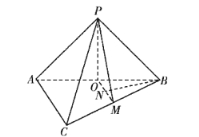
，O是AB的中點，∴
.
∵平面PAB⊥平面ABC，交線為AB，∴PO⊥平面ABC，∴PO⊥BN.
又
，∴BN⊥平面POM.
∴線段BN的長即為點B到平面POM的距離.
由△ABC是等邊三角形，可得△BOM也是等邊三角形.
∵
，∴
，
.
故點B到平面POM的距離為.
閱讀快車系列答案科目：高中數(shù)學 來源： 題型：
【題目】某精密儀器生產車間每天生產
個零件，質檢員小張每天都會隨機地從中抽取50個零件進行檢查是否合格，若較多零件不合格，則需對其余所有零件進行檢查．根據(jù)多年的生產數(shù)據(jù)和經驗，這些零件的長度服從正態(tài)分布
（單位：微米
），且相互獨立．若零件的長度
滿足
，則認為該零件是合格的，否則該零件不合格．
（1）假設某一天小張抽查出不合格的零件數(shù)為
，求
及的數(shù)學期望
；
（2）小張某天恰好從50個零件中檢查出2個不合格的零件，若以此頻率作為當天生產零件的不合格率．已知檢查一個零件的成本為10元，而每個不合格零件流入市場帶來的損失為260元．假設充分大，為了使損失盡量小，小張是否需要檢查其余所有零件，試說明理由．
附：若隨機變量
服從正態(tài)分布
，則
．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】我們稱n（
）元有序實數(shù)組（
，
，…，
）為n維向量，
為該向量的范數(shù).已知n維向量
，其中
，
，2，…，n.記范數(shù)為奇數(shù)的n維向量
的個數(shù)為
，這個向量的范數(shù)之和為
.
（1）求
和
的值；
（2）當n為偶數(shù)時，求，（用n表示）.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】如圖，橢圓
的長軸長為
，點
、
、
為橢圓上的三個點，為橢圓的右端點，
過中心
，且
，
．
（1）求橢圓的標準方程；
（2）設
、
是橢圓上位于直線
同側的兩個動點（異于、），且滿足
，試討論直線
與直線
斜率之間的關系，并求證直線
的斜率為定值.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】（本小題滿分12分）
已知函數(shù)
是奇函數(shù)，的定義域為
．當
時， 
．(e為自然對數(shù)的底數(shù))．
(1)若函數(shù)在區(qū)間
上存在極值點，求實數(shù)
的取值范圍；
(2)如果當x≥1時，不等式
恒成立，求實數(shù)
的取值范圍．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知菱形ABCD中，∠BAD=60°，AC與BD相交于點O．將△ABD沿BD折起，使頂點A至點M，在折起的過程中，下列結論正確的是（ ）
A.BD⊥CM
B.存在一個位置，使△CDM為等邊三角形
C.DM與BC不可能垂直
D.直線DM與平面BCD所成的角的最大值為60°
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知點A，B關于坐標原點O對稱，
，以M為圓心的圓過A，B兩點，且與直線
相切，若存在定點P，使得當A運動時，
為定值，則點P的坐標為（ ）
A.
B.
C.
D.
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
