
【題目】[選修4-4:坐標系與參數方程]
在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為 (
(![]() 為參數),以原點為極點,
為參數),以原點為極點, ![]() 軸的正半軸為極軸,以相同的長度單位建立極坐標系,曲線
軸的正半軸為極軸,以相同的長度單位建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(Ⅰ)求直線![]() 的極坐標方程和曲線
的極坐標方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)已知![]() ,直線
,直線![]() 與曲線
與曲線![]() 交于
交于![]() ,
, ![]() 兩點,若
兩點,若![]() ,求
,求![]() 的值.
的值.
科目:高中數學 來源: 題型:
【題目】《山東省高考改革試點方案》規定:從2017年秋季高中入學的新生開始,不分文理科;2020年開始,高考總成績由語數外3門統考科目和物理、化學等六門選考科目構成.將每門選考科目的考生原始成績從高到低劃分為A、B+、B、C+、C、D+、D、E共8個等級.參照正態分布原則,確定各等級人數所占比例分別為3%、7%、16%、24%、24%、16%、7%、3%.選考科目成績計入考生總成績時,將A至E等級內的考生原始成績,依照等比例轉換法則,分別轉換到[91,100]、[81,90]、[71,80]、[61,70]、[51,60]、[41,50]、[31,40]、[21,30]八個分數區間,得到考生的等級成績.
某校高一年級共2000人,為給高一學生合理選科提供依據,對六個選考科目進行測試,其中物理考試原始成績基本服從正態分布N(60,169).
(Ⅰ)求物理原始成績在區間(47,86)的人數;
(Ⅱ)按高考改革方案,若從全省考生中隨機抽取3人,記X表示這3人中等級成績在區間[61,80]的人數,求X的分布列和數學期望.
(附:若隨機變量![]() ,則
,則![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“水是生命之源”,但是據科學界統計可用淡水資源僅占地球儲水總量的![]() ,全世界近
,全世界近![]() 人口受到水荒的威脅.某市為了鼓勵居民節約用水,計劃調整居民生活用水收費方案,擬確定一個合理的月用水量標準
人口受到水荒的威脅.某市為了鼓勵居民節約用水,計劃調整居民生活用水收費方案,擬確定一個合理的月用水量標準![]() (噸):一位居民的月用水量不超過
(噸):一位居民的月用水量不超過![]() 的部分按平價收費,超出
的部分按平價收費,超出![]() 的部分按議價收費.為了了解居民用水情況,通過抽樣,獲得了某年100位居民每人的月均用水量(單位:噸),將數據按照
的部分按議價收費.為了了解居民用水情況,通過抽樣,獲得了某年100位居民每人的月均用水量(單位:噸),將數據按照![]() 分成9組,制成了如圖所示的頻率分布直方圖.
分成9組,制成了如圖所示的頻率分布直方圖.

(1)求直方圖中![]() 的值;
的值;
(2)設該市有60萬居民,估計全市居民中月均用水量不低于2.5噸的人數,并說明理由;
(3)若該市政府希望使![]() 的居民每月的用水不按議價收費,估計
的居民每月的用水不按議價收費,估計![]() 的值,并說明理由.
的值,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)若a=0時,求函數![]() 的零點;
的零點;
(2)若a=4時,求函數![]() 在區間[2,5]上的最大值和最小值;
在區間[2,5]上的最大值和最小值;
(3)當![]() 時,不等式
時,不等式![]() 恒成立,求實數a的取值范圍.
恒成立,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】正方體ABCD - A1B1C1D1的棱長為2, E、F、G分別為BC、CC1、BB1的中點,則( )
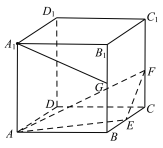
A.直線![]() 與直線AF垂直B.直線A1G與平面AEF平行
與直線AF垂直B.直線A1G與平面AEF平行
C.平面![]() 截正方體所得的截面面積為
截正方體所得的截面面積為![]() D.點C與點G到平面AEF的距離相等
D.點C與點G到平面AEF的距離相等
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com