
| x |
| x |
| a |
| x |
| 2x2-x-a |
| x |
| 1 |
| 8 |
| 1 |
| 8 |
1+
| ||
| 4 |
1-
| ||
| 4 |
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 8 |
| x |
| x |
| x |
| x |
| x |
| 2 |
| x |
| 1 | ||
|
(
| ||||||
| x |
| x |
| x |
| x |
| x | (0,1) | 1 | (1,+∞) |
| F′(x) | - | 0 | + |
| F′(x) | 遞減 | 0 | 遞增 |


 口算心算速算應用題系列答案
口算心算速算應用題系列答案 同步拓展閱讀系列答案
同步拓展閱讀系列答案科目:高中數學 來源: 題型:
| x2 |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
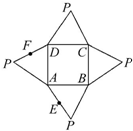 如圖是一幾何體的平面展開圖,其中ABCD為正方形,E,F分別為PA,PD的中點,在此幾何體中,給出下面四個結論:
如圖是一幾何體的平面展開圖,其中ABCD為正方形,E,F分別為PA,PD的中點,在此幾何體中,給出下面四個結論:查看答案和解析>>
科目:高中數學 來源: 題型:
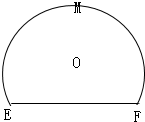 如圖,一塊弓形薄鐵片EAF,點M為
如圖,一塊弓形薄鐵片EAF,點M為 |
| EF |
| 2π |
| 3 |
 |
| EF |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com