
 ,β=arctan
,β=arctan ,γ=arcos(-
,γ=arcos(- ),δ=arccot(-
),δ=arccot(- ),則( )
),則( )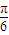 <
<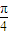 <β<
<β<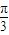 且γ<
且γ<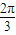 <
< <δ<
<δ<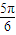 .由f(x)=x2-πx的圖象是開口向上的拋物線,其對稱軸為x=
.由f(x)=x2-πx的圖象是開口向上的拋物線,其對稱軸為x= ,討論α、β、γ和δ與對稱軸的遠近,即可得到f(γ)<f(β)<f(δ)<f(α),從而得到本題的答案.
,討論α、β、γ和δ與對稱軸的遠近,即可得到f(γ)<f(β)<f(δ)<f(α),從而得到本題的答案. <arcsin
<arcsin =
= ,arctan1=
,arctan1=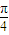 <arctan
<arctan <arctan
<arctan =
=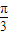
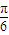 <
< <β<
<β<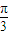
 )<arcos(-
)<arcos(- )=
)= ,
,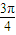 =arccot(-1)<arccot(-
=arccot(-1)<arccot(- )<arccot(-
)<arccot(-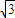 )=
)= ,
,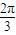 <
< <δ<
<δ< .
.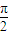 ,
,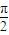 距離越近的自變量對應的函數值越小
距離越近的自變量對應的函數值越小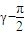 |
| <|
<| |<
|< <|
<|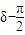 |<
|<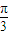 <|
<|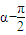 |
|

科目:高中數學 來源: 題型:
| 4 |
| x |
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com