
【題目】為了引導居民合理用水,某市決定全面實施階梯水價.階梯水價原則上以住宅(一套住宅為一戶)的月用水量為基準定價,具體劃分標準如表:
階梯級別 | 第一階梯水量 | 第二階梯水量 | 第三階梯水量 |
月用水量范圍(單位:立方米) |
|
|
|
從本市隨機抽取了10戶家庭,統計了同一月份的月用水量,得到如圖莖葉圖:
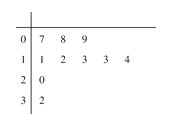
(Ⅰ)現要在這10戶家庭中任意選取3戶,求取到第二階梯水量的戶數X的分布列與數學期望;
(Ⅱ)用抽到的10戶家庭作為樣本估計全市的居民用水情況,從全市依次隨機抽取10戶,若抽到![]() 戶月用水量為一階的可能性最大,求
戶月用水量為一階的可能性最大,求![]() 的值.
的值.
【答案】(1)見解析(2)![]()
【解析】
(Ⅰ)由莖葉圖計算,可得第二階段水量的戶數![]() 的可能取值為
的可能取值為![]() ,求解隨機變量取每個值對應的概率,列出隨機變量的分布列,利用公式,求解數學期望;
,求解隨機變量取每個值對應的概率,列出隨機變量的分布列,利用公式,求解數學期望;
(Ⅱ)設![]() 為從全市抽取的10戶中用水量為一階的家庭戶數,依題意得
為從全市抽取的10戶中用水量為一階的家庭戶數,依題意得![]() ,根據概率公式,列出不等式組,求得實數
,根據概率公式,列出不等式組,求得實數![]() 的范圍,即可求解
的范圍,即可求解![]() 的值,得到答案.
的值,得到答案.
(Ⅰ)由莖葉圖可知抽取的10戶中用水量為一階的有3戶,二階的有5戶,三階的有2戶.第二階段水量的戶數![]() 的可能取值為0,1,2,3,
的可能取值為0,1,2,3,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
所以![]() 的分布列為
的分布列為
| 0 | 1 | 2 | 3 |
|
|
|
|
|
![]() 的數學期望
的數學期望![]() .
.
(Ⅱ)設![]() 為從全市抽取的10戶中用水量為一階的家庭戶數,依題意得
為從全市抽取的10戶中用水量為一階的家庭戶數,依題意得![]() ,
,
![]() ,
,
由 ,解得
,解得![]() ,又
,又![]() ,所以當
,所以當![]() 時概率最大.
時概率最大.
即從全市依次隨機抽取10戶,抽到3戶月用水量為一階的可能性最大.


科目:高中數學 來源: 題型:
【題目】某校研究性學習小組發現,學生上課的注意力指標隨著聽課時間的變化而變化.老師講課開始時學生的興趣激增,接下來學生的興趣將保持較理想的狀態一段時間,隨后學生的注意力開始分散.該小組發現注意力指標![]() 與上課時刻第
與上課時刻第![]() 分鐘末的關系如下(
分鐘末的關系如下(![]() ,設上課開始時,t=0):
,設上課開始時,t=0): .若上課后第5分鐘末時的注意力指標為140.
.若上課后第5分鐘末時的注意力指標為140.
(1)求![]() 的值;
的值;
(2)上課后第5分鐘末和第35分鐘末比較,哪個時刻注意力更集中?
(3)在一節課中,學生的注意力指標至少達到140的時間能保持多長?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】氣象意義上,從春季進入夏季的標志為:“連續5天的日平均溫度不低于22℃”.現有甲、乙、丙三地連續5天的日平均溫度的記錄數據(記錄數據都是正整數):
①甲地:5個數據的中位數為24,眾數為22;
②乙地:5個數據的中位數為27,總體均值為24;
③丙地:5個數據的中有一個數據是32,總體均值為26,總體方差為10.8;
則肯定進入夏季的地區的有( )
A. ①②③ B. ①③ C. ②③ D. ①
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列![]() 的前
的前![]() 項的和為
項的和為![]() ,且
,且![]() ,
,![]() .
.
(1)證明數列![]() 為等比數列,并求出數列
為等比數列,并求出數列![]() 的通項公式;
的通項公式;
(2)設![]() ,求數列
,求數列![]() 的前
的前![]() 項的和
項的和![]() ;
;
(3)設函數![]() (
(![]() 為常數),且(2)中的
為常數),且(2)中的![]() >
>![]() 對任意的
對任意的![]() 和
和![]() 都成立,求實數
都成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知常數![]() ,數列
,數列![]() 的前n項和為
的前n項和為![]() ,
,![]() ,
,![]() .
.
(1)求數列![]() 的通項公式;
的通項公式;
(2)若![]() ,且數列
,且數列![]() 是單調遞增數列,求實數a的取值范圍;
是單調遞增數列,求實數a的取值范圍;
(3)若![]() ,
,![]() ,對于任意給定的正整數k,是否都存在正整數p、q,使得
,對于任意給定的正整數k,是否都存在正整數p、q,使得![]() ?若存在,試求出p、q的一組值(不論有多少組,只要求出一組即可);若不存在,請說明理由.
?若存在,試求出p、q的一組值(不論有多少組,只要求出一組即可);若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,A,B是圓O:
中,A,B是圓O:![]() 與x軸的兩個交點(點B在點A右側),點
與x軸的兩個交點(點B在點A右側),點![]() ,x軸上方的動點P使直線
,x軸上方的動點P使直線![]() ,
,![]() ,
,![]() 的斜率存在且依次成等差數列.
的斜率存在且依次成等差數列.

(1)求證:動點P的橫坐標為定值;
(2)設直線![]() ,
,![]() 與圓O的另一個交點分別為S,T.求證:點Q,S,T三點共線.
與圓O的另一個交點分別為S,T.求證:點Q,S,T三點共線.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com