
【題目】我們在求高次方程或超越方程的近似解時常用二分法求解,在實際生活中還有三分法.比如借助天平鑒別假幣.有三枚形狀大小完全相同的硬幣,其中有一假幣(質量較輕),把兩枚硬幣放在天平的兩端,若天平平衡,則剩余一枚為假幣,若天平不平衡,較輕的一端放的硬幣為假幣.現有 27 枚這樣的硬幣,其中有一枚是假幣(質量較輕),如果只有一臺天平,則一定能找到這枚假幣所需要使用天平的最少次數為( )
A.2B.3C.4D.5
【答案】B
【解析】
根據提示三分法,考慮將硬幣分為![]() 組,然后將有問題的一組再分為
組,然后將有問題的一組再分為![]() 組,再將其中有問題的一組分為
組,再將其中有問題的一組分為![]() ,此時每組僅為
,此時每組僅為![]() 枚硬幣,即可分析出哪一個是假幣.
枚硬幣,即可分析出哪一個是假幣.
第一步將27枚硬幣分為三組,每組9枚,取兩組分別放于天平左右兩側測量,若天平平衡,則假幣在第三組中;若天平不平衡,假幣在較輕的那一組中;第二步把較輕的9枚金幣再分成三組,每組3枚,任取2組,分別放于天平左右兩側測量,若天平平衡,則假幣在第三組,若天平不平衡則假幣在較輕的一組;第三步再將假幣所在的一組分成三組,每組1枚,取其中兩組放于天平左右兩側測量若天平平衡,則假幣是剩下的一個;若天平不平衡,則較輕的盤中所放的為假幣.因此,一定能找到假幣最少需使用3次天平.
故選:B.


 特高級教師點撥系列答案
特高級教師點撥系列答案科目:高中數學 來源: 題型:
【題目】下列說法錯誤的是( )
A. 命題![]() :存在
:存在![]() ,使
,使![]() ,則非
,則非![]() :對任意
:對任意![]() ,都有
,都有![]() ;
;
B. 如果命題“![]() 或
或![]() ”與命題“非
”與命題“非![]() ”都是真命題,那么命題
”都是真命題,那么命題![]() 一定是真命題;
一定是真命題;
C. 命題“若![]() 都是偶數,則
都是偶數,則![]() 是偶數”的逆否命題是“若
是偶數”的逆否命題是“若![]() 不是偶數,則
不是偶數,則![]() 不是偶數”;
不是偶數”;
D. 命題“存在![]() ,
,![]() ”是假命題
”是假命題
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】假設某種設備使用的年限![]() (年)與所支出的維修費用
(年)與所支出的維修費用![]() (萬元)有以下統計資料:
(萬元)有以下統計資料:
使用年限 | 2 | 3 | 4 | 5 | 6 |
維修費用 | 2 | 4 | 5 | 6 | 7 |
若由資料知![]() 對
對![]() 呈線性相關關系.試求:
呈線性相關關系.試求:
(1)求![]() ;
;
(2)線性回歸方程![]() ;
;
(3)估計使用10年時,維修費用是多少?
附:利用“最小二乘法”計算![]() 的值時,可根據以下公式:
的值時,可根據以下公式: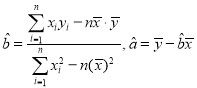
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】汽車尾氣中含有一氧化碳(![]() ),碳氫化合物(
),碳氫化合物(![]() )等污染物,是環境污染的主要因素之一,汽車在使用若干年之后排放的尾氣中的污染物會出現遞增的現象,所以國家根據機動車使用和安全技術、排放檢驗狀況,對達到報廢標準的機動車實施強制報廢.某環保組織為了解公眾對機動車強制報廢標準的了解情況,隨機調查了100人,所得數據制成如下列聯表:
)等污染物,是環境污染的主要因素之一,汽車在使用若干年之后排放的尾氣中的污染物會出現遞增的現象,所以國家根據機動車使用和安全技術、排放檢驗狀況,對達到報廢標準的機動車實施強制報廢.某環保組織為了解公眾對機動車強制報廢標準的了解情況,隨機調查了100人,所得數據制成如下列聯表:
不了解 | 了解 | 總計 | |
女性 |
|
| 50 |
男性 | 15 | 35 | 50 |
總計 |
|
| 100 |
(1)若從這100人中任選1人,選到了解機動車強制報廢標準的人的概率為![]() ,問是否有
,問是否有![]() 的把握認為“對機動車強制報廢標準是否了解與性別有關”?
的把握認為“對機動車強制報廢標準是否了解與性別有關”?
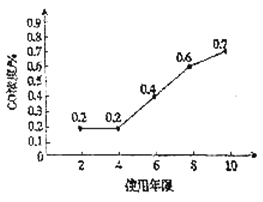
(2)該環保組織從相關部門獲得某型號汽車的使用年限與排放的尾氣中![]() 濃度的數據,并制成如圖所示的折線圖,若該型號汽車的使用年限不超過15年,可近似認為排放的尾氣中
濃度的數據,并制成如圖所示的折線圖,若該型號汽車的使用年限不超過15年,可近似認為排放的尾氣中![]() 濃度
濃度![]() 與使用年限
與使用年限![]() 線性相關,試確定
線性相關,試確定![]() 關于
關于![]() 的回歸方程,并預測該型號的汽車使用12年排放尾氣中的
的回歸方程,并預測該型號的汽車使用12年排放尾氣中的![]() 濃度是使用4年的多少倍.
濃度是使用4年的多少倍.
附: (
(![]() )
)
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
參考公式:用最小二乘法求線性回歸方程系數公式: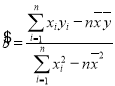 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我們在求高次方程或超越方程的近似解時常用二分法求解,在實際生活中還有三分法.比如借助天平鑒別假幣.有三枚形狀大小完全相同的硬幣,其中有一假幣(質量較輕),把兩枚硬幣放在天平的兩端,若天平平衡,則剩余一枚為假幣,若天平不平衡,較輕的一端放的硬幣為假幣.現有 27 枚這樣的硬幣,其中有一枚是假幣(質量較輕),如果只有一臺天平,則一定能找到這枚假幣所需要使用天平的最少次數為( )
A.2B.3C.4D.5
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠擬建一座平面圖(如右圖所示)為矩形且面積為200平方米的三級污水處理池,由于地形限制,長、寬都不能超過16米,如果池外周壁建造單價為每米400元,中間兩條隔墻建造單價為每米248元,池底建造單價為每平方米80元(池壁厚度忽略不計,且池無蓋).

(1)寫出總造價y(元)與污水處理池長x(米)的函數關系式,并指出其定義域;
(2)求污水處理池的長和寬各為多少時,污水處理池的總造價最低?并求最低總造價.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設某工廠生產的一種產品的一項質量指標值![]() 服從正態分布
服從正態分布![]() ,若一件產品的質量指標值
,若一件產品的質量指標值![]() 介于90到120之間時,稱該產品為優質品.
介于90到120之間時,稱該產品為優質品.
(1)計算該工廠生產的這種產品的優質品率![]() .
.
(2)某用戶從該工廠購買了100件這種產品,記![]() 表示這100件產品中優質品的件數,求隨機變量
表示這100件產品中優質品的件數,求隨機變量![]() 的數學期望
的數學期望![]() .
.
(3)必須從這工廠中購買多少件產品,才能使其中至少有1件產品是優質品的概率大于0.9?
①參考數據:若隨機變量![]() ),則
),則![]() ,
,![]() ,
,![]() .
.
②計算時,所有的小數都精確到小數點后4位,例如:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】雙曲線![]() 與橢圓
與橢圓![]() 有相同的焦點,直線
有相同的焦點,直線![]() 為雙曲線
為雙曲線![]() 的一條漸近線.
的一條漸近線.
(1)求雙曲線![]() 的方程;
的方程;
(2)過點![]() 的直線
的直線![]() 交雙曲線
交雙曲線![]() 于
于![]() 、
、![]() 兩點,交
兩點,交![]() 軸于
軸于![]() 點(
點(![]() 點與
點與![]() 的頂點不重合),當
的頂點不重合),當![]() ,且
,且![]() ,求
,求![]() 點的坐標.
點的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com