
【題目】已知函數![]() (
(![]() 為自然對數的底,
為自然對數的底,![]() 為常數,
為常數,![]() )有兩個極值點
)有兩個極值點![]() ,且
,且![]() .
.
(Ⅰ)求![]() 的取值范圍;
的取值范圍;
(Ⅱ)若![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
(Ⅰ)首先通過導數運算將極值點問題轉化為方程解的問題,從而轉化成兩個函數圖像交點問題,再根據導數的應用確定函數的極值點、單調性,從而畫出簡圖,判斷出所求范圍;(Ⅱ)首先根據隱含條件消元,將不等式轉化為關于![]() 的不等式,從而構造函數,建立函數模型,再通過分類討論該函數的單調性,確定實數
的不等式,從而構造函數,建立函數模型,再通過分類討論該函數的單調性,確定實數![]() 的取值范圍.
的取值范圍.
(Ⅰ)![]() ,由
,由![]() 得
得![]() ,
,
依題意,該方程有兩個不同正實數根,記![]() ,則
,則![]() ,
,
當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ,
,
所以函數![]() 在
在![]() 處取得最小值
處取得最小值![]() ,所以
,所以![]() 的取值范圍是
的取值范圍是![]() .
.
(Ⅱ)由(Ⅰ)得:![]() ,且
,且![]() ,所以
,所以![]() ,
,![]() ,所以
,所以![]() ,
,
因此![]() 恒成立,即
恒成立,即![]() 恒成立,
恒成立,
即![]() ,設
,設![]() ,即
,即![]() 在
在![]() 上恒成立,
上恒成立,
從而![]() ,記
,記![]() ,
,![]() ,
,![]()
![]() ,
,
① 當![]() 時,
時,![]() ,所以
,所以![]() ,從而
,從而![]() ,
,
則![]() 在區間
在區間![]() 上單調遞減,所以當
上單調遞減,所以當![]() 時,
時,![]() 恒成立;
恒成立;
② ![]() 時,
時,![]() 等價于
等價于![]() ,
,![]() ,
,
所以![]() 有兩根
有兩根![]() ,且
,且![]() ,可以不妨設
,可以不妨設![]() ,
,
![]() 在
在![]() 時成立,所以
時成立,所以![]() 在區間
在區間![]() 上單調遞增,當
上單調遞增,當![]() 時,
時,![]() ,即
,即![]() 在
在![]() 上不恒成立,
上不恒成立,
綜上,![]() 的取值范圍是
的取值范圍是![]() .
.


科目:高中數學 來源: 題型:
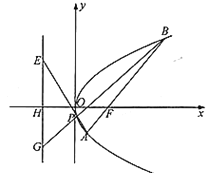
【題目】已知拋物線![]() :
:![]() 的焦點為
的焦點為![]() ,過
,過![]() 且斜率為
且斜率為![]() 的直線
的直線![]() 與拋物線
與拋物線![]() 交于
交于![]() ,
,![]() 兩點,
兩點,![]() 在
在![]() 軸的上方,且點
軸的上方,且點![]() 的橫坐標為4.
的橫坐標為4.
(1)求拋物線![]() 的標準方程;
的標準方程;
(2)設點![]() 為拋物線
為拋物線![]() 上異于
上異于![]() ,
,![]() 的點,直線
的點,直線![]() 與
與![]() 分別交拋物線
分別交拋物線![]() 的準線于
的準線于![]() ,
,![]() 兩點,
兩點,![]() 軸與準線的交點為
軸與準線的交點為![]() ,求證:
,求證:![]() 為定值,并求出定值.
為定值,并求出定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某分公司經銷某種品牌產品,每件產品的成本為30元,并且每件產品須向總公司繳納![]() 元(
元(![]() 為常數,
為常數,![]() )的管理費.根據多年的統計經驗,預計當每件產品的售價為
)的管理費.根據多年的統計經驗,預計當每件產品的售價為![]() 元時,產品一年的銷售量為
元時,產品一年的銷售量為![]() 為自然對數的底數)萬件.已知每件產品的售價為40元時,該產品一年的銷售量為500萬件.經物價部門核定每件產品的售價
為自然對數的底數)萬件.已知每件產品的售價為40元時,該產品一年的銷售量為500萬件.經物價部門核定每件產品的售價![]() 最低不低于35元,最高不超過41元.
最低不低于35元,最高不超過41元.
(Ⅰ)求分公司經營該產品一年的利潤![]() 萬元與每件產品的售價
萬元與每件產品的售價![]() 元的函數關系式;
元的函數關系式;
(Ⅱ)當每件產品的售價為多少元時,該產品一年的利潤![]() 最大,并求
最大,并求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】據史載知,新華網:北京2008年11月9日電,國務院總理溫家寶主持召開國務院常務會議.研究部署進一步擴大內需促進經濟平穩較快增長的措施,以應對日趨嚴峻的全球性世界經濟金融危機,在提高城鄉居民特別是低收入人群的收入水平政策措施的刺激下,某零售店當時近5個月的銷售額和利潤額數據統計如下表:
月份 | 2 | 3 | 4 | 5 | 6 |
銷售額x/千萬元 | 3 | 5 | 6 | 7 | 9 |
利潤額y/百萬元 | 2 | 3 | 3 | 4 | 5 |
(1)若x與y之間是線性相關關系,求利潤額y關于銷售額x的線性回歸方程![]() ;
;
(2)若9月份的銷售額為8千萬元,試利用(1)的結論估計該零售店9月份的利潤額.
參考公式: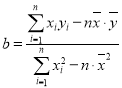 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設A,B為曲線C:![]() 上兩點,A與B的橫坐標之和為4.
上兩點,A與B的橫坐標之和為4.
(1)求直線AB的斜率;
(2)設M為曲線C上一點,C在M處的切線與直線AB平行,且AM⊥BM,求直線AB的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有一個底面半徑為3,軸截面為正三角形的圓錐紙盒,在該紙盒內放一個棱長均為a的四面體,并且四面體在紙盒內可以任意轉動,則a的最大值為________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com