
【題目】某總公司在A,B兩地分別有甲、乙兩個下屬公司同時生產某種新能源產品(這兩個公司每天都固定生產50件產品),所生產的產品均在本地銷售.產品進入市場之前需要對產品進行性能檢測,得分低于80分的定為次品,需要返廠再加工;得分不低于80分的定為正品,可以進入市場.檢測員統計了甲、乙兩個下屬公司100天的生產情況及每件產品盈利虧損情況,數據如下表所示:
表1:
甲公司 | 得分 |
|
|
|
|
|
件數 | 10 | 10 | 40 | 40 | 50 | |
天數 | 10 | 10 | 10 | 10 | 80 |
表2:
乙公司 | 得分 |
|
|
|
| |
件數 | 10 | 5 | 40 | 45 | 50 | |
天數 | 20 | 10 | 20 | 10 | 70 |
表3:
每件正品 | 每件次品 | |
甲公司 | 盈2萬元 | 虧3萬元 |
乙公司 | 盈3萬元 | 虧3.5萬元 |
(1)分別求甲、乙兩個公司這100天生產的產品的正品率(用百分數表示);
(2)試問甲乙兩個公司這100天生產的產品的總利潤哪個更大?說明理由.
科目:高中數學 來源: 題型:
【題目】某水果批發商經銷某種水果(以下簡稱![]() 水果),購入價為300元/袋,并以360元/袋的價格售出,若前8小時內所購進的
水果),購入價為300元/袋,并以360元/袋的價格售出,若前8小時內所購進的![]() 水果沒有售完,則批發商將沒售完的
水果沒有售完,則批發商將沒售完的![]() 水果以220元/袋的價格低價處理完畢(根據經驗,2小時內完全能夠把
水果以220元/袋的價格低價處理完畢(根據經驗,2小時內完全能夠把![]() 水果低價處理完,且當天不再購入).該水果批發商根據往年的銷量,統計了100天
水果低價處理完,且當天不再購入).該水果批發商根據往年的銷量,統計了100天![]() 水果在每天的前8小時內的銷售量,制成如下頻數分布條形圖.
水果在每天的前8小時內的銷售量,制成如下頻數分布條形圖.

記![]() 表示
表示![]() 水果一天前8小時內的銷售量,
水果一天前8小時內的銷售量,![]() 表示水果批發商一天經營
表示水果批發商一天經營![]() 水果的利潤,
水果的利潤,![]() 表示水果批發商一天批發
表示水果批發商一天批發![]() 水果的袋數.
水果的袋數.
(1)若![]() ,求
,求![]() 與
與![]() 的函數解析式;
的函數解析式;
(2)假設這100天中水果批發商每天購入![]() 水果15袋或者16袋,分別計算該水果批發商這100天經營
水果15袋或者16袋,分別計算該水果批發商這100天經營![]() 水果的利潤的平均數,以此作為決策依據,每天應購入
水果的利潤的平均數,以此作為決策依據,每天應購入![]() 水果15袋還是16袋?
水果15袋還是16袋?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的四個頂點圍成的菱形的面積為
的四個頂點圍成的菱形的面積為![]() ,橢圓的一個焦點為
,橢圓的一個焦點為![]() .
.
(1)求橢圓的方程;
(2)若![]() ,
,![]() 為橢圓上的兩個動點,直線
為橢圓上的兩個動點,直線![]() ,
,![]() 的斜率分別為
的斜率分別為![]() ,
,![]() ,當
,當![]() 時,
時,![]() 的面積是否為定值?若為定值,求出此定值;若不為定值,說明理由.
的面積是否為定值?若為定值,求出此定值;若不為定值,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著疫情的有效控制,人們的生產生活逐漸向正常秩序恢復,位于我區的某著名賞花園區重新開放.據統計硏究,近期每天賞花的人數大致符合以下數學模型![]() .以
.以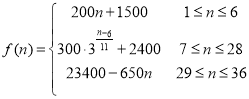 表示第
表示第![]() 個時刻進入園區的人數,以
個時刻進入園區的人數,以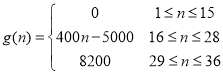 表示第
表示第![]() 個時刻離開園區的人數,設定每15分鐘為一個計算單位,上午8點15分作為第1個計算人數單位,即
個時刻離開園區的人數,設定每15分鐘為一個計算單位,上午8點15分作為第1個計算人數單位,即![]() 點30分作為第2個計算單位,即
點30分作為第2個計算單位,即![]() :依次類推,把一天內從上午8點到下午5點分成36個計算單位(最后結果四舍五入,精確到整數)
:依次類推,把一天內從上午8點到下午5點分成36個計算單位(最后結果四舍五入,精確到整數)
(1)試分別計算當天12:30至13:30這一小時內,進入園區的人數![]() 和離開園區的游客人數
和離開園區的游客人數![]() .
.
(2)請問,從12點(即![]() )開始,園區內總人數何時達到最多?并說明理由
)開始,園區內總人數何時達到最多?并說明理由
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國古代數學名著《算法統宗》中有如下問題:“遠望巍巍塔七層,紅光點點倍加增,共燈三百八十一,請問尖頭幾盞燈?”意思是:一座7層塔共掛了381盞燈,且相鄰兩層中的下一層燈數是上一層燈數的2倍,則塔的頂層共有燈( )
A. 1盞 B. 3盞 C. 5盞 D. 9盞
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“難度系數”反映試題的難易程度,難度系數越大,題目得分率越高,難度也就越小.“難度系數”的計算公式為![]() ,其中,
,其中,![]() 為難度系數,
為難度系數,![]() 為樣本平均失分,
為樣本平均失分,![]() 為試卷總分(一般為100分或150分).某校高三年級的李老師命制了某專題共5套測試卷(每套總分150分),用于對該校高三年級480名學生進行每周測試.測試前根據自己對學生的了解,預估了每套試卷的難度系數,如下表所示:
為試卷總分(一般為100分或150分).某校高三年級的李老師命制了某專題共5套測試卷(每套總分150分),用于對該校高三年級480名學生進行每周測試.測試前根據自己對學生的了解,預估了每套試卷的難度系數,如下表所示:
試卷序號 | 1 | 2 | 3 | 4 | 5 |
考前預估難度系數 | 0.7 | 0.64 | 0.6 | 0.6 | 0.55 |
測試后,隨機抽取了50名學生的數據進行統計,結果如下:
試卷序號 | 1 | 2 | 3 | 4 | 5 |
實測平均分 | 102 | 99 | 93 | 93 | 87 |
(1)根據試卷2的難度系數估計這480名學生第2套試卷的平均分;
(2)從抽樣的50名學生的5套試卷中隨機抽取2套試卷,記這2套試卷中平均分超過96分的套數為![]() ,求
,求![]() 的分布列和數學期望;
的分布列和數學期望;
(3)試卷的預估難度系數和實測難度系數之間會有偏差.設![]() 為第
為第![]() 套試卷的實測難度系數,并定義統計量
套試卷的實測難度系數,并定義統計量![]() ,若
,若![]() ,則認為本專題的5套試卷測試的難度系數預估合理,否則認為不合理.試檢驗本專題的5套試卷對難度系數的預估是否合理.
,則認為本專題的5套試卷測試的難度系數預估合理,否則認為不合理.試檢驗本專題的5套試卷對難度系數的預估是否合理.
查看答案和解析>>
科目:高中數學 來源: 題型:
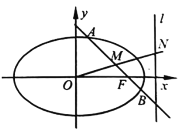
【題目】已知橢圓![]() 的右焦點為
的右焦點為![]() ,右準線為
,右準線為![]() .過點
.過點![]() 作與坐標軸都不垂直的直線與橢圓
作與坐標軸都不垂直的直線與橢圓![]() 交于
交于![]() ,
,![]() 兩點,線段
兩點,線段![]() 的中點為
的中點為![]() ,
,![]() 為坐標原點,且直線
為坐標原點,且直線![]() 與右準線
與右準線![]() 交于點
交于點![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若![]() ,求直線
,求直線![]() 的方程;
的方程;
(3)是否存在實數![]() ,使得
,使得![]() 恒成立?若存在,求實數
恒成立?若存在,求實數![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某地有一塊半徑為R的扇形AOB公園,其中O為扇形所在圓的圓心,AOB=![]() ,OA,OB,
,OA,OB,![]() 為公園原有道路.為滿足市民觀賞和健身的需要,市政部門擬在
為公園原有道路.為滿足市民觀賞和健身的需要,市政部門擬在![]() 上選取一點M,新建道路OM及與OA平行的道路MN(點N在線段OB上),設AOM=
上選取一點M,新建道路OM及與OA平行的道路MN(點N在線段OB上),設AOM=![]() .
.

(1)如何設計,才能使市民從點O出發沿道路OM,MN行走至點N所經過的路徑最長?請說明理由;
(2)如何設計,才能使市民從點A出發沿道路![]() ,MN行走至點N所經過的路徑最長?請說明理由.
,MN行走至點N所經過的路徑最長?請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com