
【題目】借助計算機(器)作某些分段函數圖象時,分段函數的表示有時可以利用函數![]() ,例如要表示分段函數g(x)=
,例如要表示分段函數g(x)=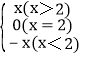 總可以將g(x)表示為g(x)=xh(x-2)+(-x)h(2-x).
總可以將g(x)表示為g(x)=xh(x-2)+(-x)h(2-x).
(1)設f(x)=(x2-2x+3)h(x-1)+(1-x2)h(1-x),請把函數f(x)寫成分段函數的形式;
(2)已知G(x)=[(3a-1)x+4a]h(1-x)+logaxh(x-1)是R上的減函數,求a的取值范圍;
(3)設F(x)=(x2+x-a+1)h(x-a)+(x2-x+a+1)h(a-x),求函數F(x)的最小值.
【答案】(1)f(x)=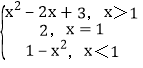 ; (2)
; (2)![]() ≤a<
≤a<![]() ; (3)當a≤-
; (3)當a≤-![]() 時,最小值為-a+
時,最小值為-a+![]() ;當a≥
;當a≥![]() 時,最小值為為a+
時,最小值為為a+![]() ;當-
;當-![]() <a<
<a<![]() 時,最小值為F(a)=a2+1.
時,最小值為F(a)=a2+1.
【解析】
(1)分當x>1、當x=1和當x<1時3種情況加以討論,分別根據函數的對應法則代入,可得f(x)相應范圍內的表達式,最后綜合可得函數f(x)寫成分段函數的形式;
(2)運用分段函數形式表示G(x),再由一次函數、對數函數的單調性,可得a的范圍;
(3)由題意,討論x>a,x=a,x<a,求得F(x)的解析式,再結合二次函數的圖象與性質,分a![]() 、
、![]() a
a![]() 和a
和a![]() 的4種情況進行討論,最后綜合可得F(x)的最小值.
的4種情況進行討論,最后綜合可得F(x)的最小值.
(1)當x>1時,x-1>0,1-x<0,可得f(x)=(x2-2x+3)+0(1-x2)=x2-2x+3;
當x=1時,f(x)=2;
當x<1時,x-1<0,1-x>0,可得f(x)=1-x2.
即有f(x)=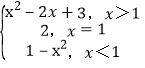 ;
;
(2)G(x)=[(3a-1)x+4a]h(1-x)+logaxh(x-1)
=![]() ,
,
由y=G(x)是R上的減函數,
可得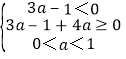 ,
,
解得![]() ≤a<
≤a<![]() ;
;
(3)F(x)=(x2+x-a+1)h(x-a)+(x2-x+a+1)h(a-x),
當x>a時,x-a>0,可得F(x)=x2+x-a+1;
若a≥-![]() ,可得F(x)在x>a遞增,可得F(x)>F(a)=a2+1;
,可得F(x)在x>a遞增,可得F(x)>F(a)=a2+1;
若a<-![]() ,可得F(x)的最小值為F(-
,可得F(x)的最小值為F(-![]() )=
)=![]() -a;
-a;
當x=a時,可得F(x)=2(a2+1);
當x<a時,x-a<0,a-x>0,則F(x)=x2-x+a+1.
若a≥![]() ,可得F(x)在x<a的最小值為F(
,可得F(x)在x<a的最小值為F(![]() )=a+
)=a+![]() ;
;
若a<![]() ,可得F(x)在x<a遞減,即有F(x)>F(a)=a2+1.
,可得F(x)在x<a遞減,即有F(x)>F(a)=a2+1.
①當a≥![]() 時,F(x)在區(qū)間(-∞,-
時,F(x)在區(qū)間(-∞,-![]() )上單調遞減,
)上單調遞減,
在區(qū)間(-![]() ,a)上單調遞增,在區(qū)間(a,+∞)上單調遞增,
,a)上單調遞增,在區(qū)間(a,+∞)上單調遞增,
可得F(-![]() )為最小值,且為
)為最小值,且為![]() -
-![]() +a+1=a+
+a+1=a+![]() ;
;
②當-![]() <a<
<a<![]() 時,F(x)在區(qū)間(-∞,a)上單調遞減,在區(qū)間(a,+∞)上單調遞增.
時,F(x)在區(qū)間(-∞,a)上單調遞減,在區(qū)間(a,+∞)上單調遞增.
F(x)的最小值為F(a)=a2+1;
③當a≤-![]() 時,在區(qū)間(-∞,a)上單調遞減,在區(qū)間(a,-
時,在區(qū)間(-∞,a)上單調遞減,在區(qū)間(a,-![]() )上單調遞減,
)上單調遞減,
在區(qū)間(-![]() ,+∞)上單調遞增.
,+∞)上單調遞增.
所以F(x)的最小值為F(-![]() )=-a+
)=-a+![]() ;
;
綜上所述,得當a≤-![]() 時,F(x)的最小值為-a+
時,F(x)的最小值為-a+![]() ;
;
當a≥![]() 時,F(x)的最小值為為a+
時,F(x)的最小值為為a+![]() ;
;
當-![]() <a<
<a<![]() 時,F(x)的最小值為F(a)=a2+1.
時,F(x)的最小值為F(a)=a2+1.


 綜合自測系列答案
綜合自測系列答案科目:高中數學 來源: 題型:
【題目】在平面上,過點P作直線l的垂線所得的垂足稱為點P在直線l上的投影,由區(qū)域  中的點在直線x+y﹣2=0上的投影構成的線段記為AB,則|AB|=( )
中的點在直線x+y﹣2=0上的投影構成的線段記為AB,則|AB|=( )
A.2 ![]()
B.4
C.3 ![]()
D.6
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知{an}是公差為3的等差數列,數列{bn}滿足b1=1,b2= ![]() ,anbn+1+bn+1=nbn .
,anbn+1+bn+1=nbn .
(1)求{an}的通項公式;
(2)求{bn}的前n項和.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設命題p:實數x滿足(x-a)(x-3a)<0,其中a>0,命題q:實數x滿足(x-3)(x-2)≤0.
(1)若a=1,且p∧q為真,求實數x的取值范圍.
(2)若¬p是¬q的充分不必要條件,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)(x∈R)滿足f(x)=f(2﹣x),若函數y=|x2﹣2x﹣3|與 y=f(x) 圖象的交點為(x1 , y1),(x2 , y2),…,(xm , ym),則![]() xi=( )
xi=( )
A.
B.m
C.2m
D.4m
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選項4-4:坐標系與參數方程]
在直角坐標系xOy中,圓C的方程為(x+6)2+y2=25.
(1)以坐標原點為極點,x軸正半軸為極軸建立極坐標系,求C的極坐標方程;
(2)直線l的參數方程是 ![]() (t為參數),l與C交與A,B兩點,|AB|=
(t為參數),l與C交與A,B兩點,|AB|= ![]() ,求l的斜率.
,求l的斜率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本題滿分10分)已知半徑為![]() 的圓的圓心M在
的圓的圓心M在![]() 軸上,圓心M的橫坐標是整數,且圓M與直線
軸上,圓心M的橫坐標是整數,且圓M與直線![]() 相切.
相切.
求:(Ⅰ)求圓M的方程;
(Ⅱ)設直線![]() 與圓M相交于
與圓M相交于![]() 兩點,求實數
兩點,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=kax-a-x(a>0且a≠1)是R上的奇函數.
(Ⅰ)求常數k的值;
(Ⅱ)若a>1,試判斷函數f(x)的單調性,并加以證明;
(Ⅲ)若a=2,且函數g(x)=a2x+a-2x-2mf(x)在[0,1]上的最小值為1,求實數m的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com