【題目】(1)求函數
取得最大值時的自變量
的集合并說出最大值；
(2)求函數
的單調遞增區間.
【答案】（1）3；（2）
和
.
【解析】
(1)根據余弦函數的值域可求出函數
的最大值，由
，可求得 取得最大值時自變量
的集合；（2）由
，求得的范圍，可得函數
的增區間，再結合
，進一步確定函數的增區間.
(1)由2x = + 2k, 得x =
+ k, k Z.
所以, 函數y = - 3cos2x, x R取得最大值時的自變量x的集合是{x | x 
+ k, k Z}.
函數y = - 3cos2x, x R的得最大值是3.
(2)由-+ 2k 2x +
+ 2k, 得-
+ k x 
+ k, k Z.
設A = [0, ], B = {x |-+ k x + k, k Z}, 易知A∩B = [0,]∪[
, ]. 所以, 函數y = 3sin(2x +), x [0, ]的單調遞增區間為[0,]和[, ].
新活力總動員暑系列答案
龍人圖書快樂假期暑假作業鄭州大學出版社系列答案科目：高中數學 來源： 題型：
【題目】已知數列{an}滿足a1=﹣1，|an﹣an﹣1|=2n﹣1（n∈N，n≥2），且{a2n﹣1}是遞減數列，{a2n}是遞增數列，則a2016= ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某房地產開發公司計劃在一樓區內建造一個長方形公園ABCD，公園由形狀為長方形A1B1C1D1的休閑區和環公園人行道(陰影部分)組成．已知休閑區A1B1C1D1的面積為4000平方米，人行道的寬分別為4米和10米(如圖所示)．
(1)若設休閑區的長和寬的比
＝x(x>1)，求公園ABCD所占面積S關于x的函數S(x)的解析式；
(2)要使公園所占面積最小，則休閑區A1B1C1D1的長和寬該如何設計？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖放置的邊長為2的正三角形
沿
軸滾動, 設頂點
的縱坐標與橫坐標的函數關系式是
， 有下列結論:
①函數的值域是
；②對任意的
，都有
；
③函數是偶函數；④函數單調遞增區間為
.
其中正確結論的序號是________. (寫出所有正確結論的序號)
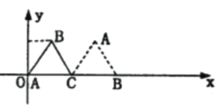
說明:
“正三角形沿軸滾動”包括沿軸正方向和沿軸負方向滾動. 沿軸正方向滾動指的是先以頂點
為中心順時針旋轉, 當頂點
落在軸上時, 再以頂點為中心順時針旋轉, 如此繼續. 類似地, 正三角形可以沿軸負方向滾動.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
，
．
（Ⅰ）若函數
在
處的切線方程為
，求
的值；
（Ⅱ）當
時，若不等式
恒成立，求
的取值范圍；
（Ⅲ）當
時，若方程
在
上總有兩個不等的實根， 求的最小值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某學校有120名教師，且年齡都在20歲到60歲之間，各年齡段人數按分組，其頻率分布直方圖如圖所示，學校要求每名教師都要參加兩項培訓，培訓結束后進行結業考試．已知各年齡段兩項培訓結業考試成績優秀的人數如表示，假設兩項培訓是相互獨立的，結業考試成績也互不影響．
年齡分組 | A項培訓成績優秀人數 | B項培訓成績優秀人數 |
[20，30） | 30 | 18 |
[30，40） | 36 | 24 |
[40，50） | 12 | 9 |
[50，60] | 4 | 3 |
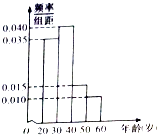
（1）若用分層抽樣法從全校教師中抽取一個容量為40的樣本，求從年齡段[20，30）抽取的人數；
（2）求全校教師的平均年齡；
（3）隨機從年齡段[20，30）和[30，40）內各抽取1人，設這兩人中兩項培訓結業考試成績都優秀的人數為X，求X的概率分布和數學期望．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，正方形
內的圖形來自中國古代的太極圖.正方形內切圓中的黑色部分和白色部分位于正方形的中心成中心對稱，在正方形內隨機取一點，則此點取自黑色部分的概率是( )
A. 
B. 
C. 
D. 
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
