
 a、c∈R滿足條件:①f(1)=0;②對一切x∈R,都有f(x)≥0.
a、c∈R滿足條件:①f(1)=0;②對一切x∈R,都有f(x)≥0. 是二次函數,再利用二次函數的性質解決對一切x∈R,都有f(x)≥0;根據f(1)=0得
是二次函數,再利用二次函數的性質解決對一切x∈R,都有f(x)≥0;根據f(1)=0得 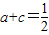 ,即
,即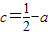 ,從而可得
,從而可得  ,進而可得
,進而可得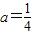 ,
, ,
,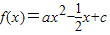 是二次函數,再利用二次函數的性質解決對一切x∈R,都有f(x)≥0;由f(1)=0,得
是二次函數,再利用二次函數的性質解決對一切x∈R,都有f(x)≥0;由f(1)=0,得  ,代入上式得
,代入上式得  ,根據
,根據  ,可得
,可得 ,從而有
,從而有  ,故可求a、c的值;
,故可求a、c的值;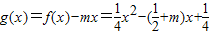 .該函數圖象開口向上,且對稱軸為x=2m+1.假設存在實數m使函數
.該函數圖象開口向上,且對稱軸為x=2m+1.假設存在實數m使函數 在區間[m,m+2]上有最小值-5.根據函數的對稱軸與區間的關系進行分類討論,從而可求m的值
在區間[m,m+2]上有最小值-5.根據函數的對稱軸與區間的關系進行分類討論,從而可求m的值 .
. ,即
,即 ,∴
,∴ .
. 是二次函數. …(2分)
是二次函數. …(2分)
 (*)…(4分)
(*)…(4分) ,即
,即 ,代入(*)得
,代入(*)得  .
. ,即
,即 .
. ,∴
,∴ .
. 代入(*)得,
代入(*)得, ,
,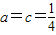 . …(7分)
. …(7分)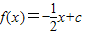 .
. ,即
,即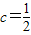 ,
, .
. 是二次函數. …(2分)
是二次函數. …(2分)
 …(4分)
…(4分) .
. ,代入上式得
,代入上式得  .
. ,
, .
.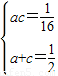 解得
解得  . …(7分)
. …(7分)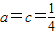 ,∴
,∴ .
. .
. 在區間[m,m+2]上有最小值-5.
在區間[m,m+2]上有最小值-5. ,
, .
. >-1,∴m=
>-1,∴m= 舍去. …(10分)
舍去. …(10分) .
. 或m=
或m= ,均應舍去. …(12分)
,均應舍去. …(12分)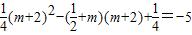 .
. 或m=
或m=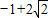 ,其中m=
,其中m=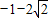 應舍去.
應舍去.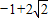 時,函數g(x)=f(x)-mx在區間[m,m+2]上有最小值-5.
時,函數g(x)=f(x)-mx在區間[m,m+2]上有最小值-5.

科目:高中數學 來源: 題型:

A、{x|
| ||
B、{x|
| ||
| C、{x|1<x<2} | ||
| D、{x|1<x<5} |
查看答案和解析>>
科目:高中數學 來源: 題型:
| b |
| a |
查看答案和解析>>
科目:高中數學 來源: 題型:單選題

 <x<4}
<x<4} <x<3}
<x<3}查看答案和解析>>
科目:高中數學 來源:2010年高考數學專項復習:不等式(解析版) 題型:選擇題

 <x<4}
<x<4} <x<3}
<x<3}查看答案和解析>>
科目:高中數學 來源:2011屆湖北省襄陽五中高三第四次模擬考試文科數學 題型:單選題
已知 是定義域為R的奇函數,
是定義域為R的奇函數, ,
, 的導函數
的導函數 的圖象如圖所示.若兩正數
的圖象如圖所示.若兩正數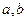 滿 足
滿 足 ,則
,則 的取值范圍是( )
的取值范圍是( )
A. | B.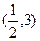 | C. | D.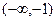 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com