Question

已知集合A={（x，y）|y=|x-1|，x，y∈R}，B={（x，y）|y=ax+2，x，y∈R}，若集合A∩B有且只有一個元素，則實數a的取值范圍是    ．

Answer 1

【答案】分析：由條件“集合A∩B有且只有一個元素”可聯立方程組轉化成方程只有一解，再轉化成兩個函數圖象只有一個交點，結合圖象即可得到實數a的取值范圍．
解答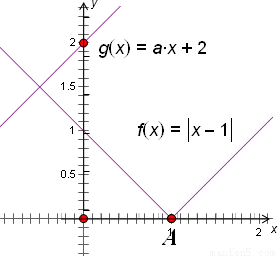：解：∵集合A與集合B都是點集，集合A∩B有且只有一個元素
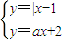
∴方程組有且只有一個解
結合函數的圖象
可知：實數a的取值范圍是 （-∞，-1]∪[1，+∞），
故答案為（-∞，-1]∪[1，+∞）
點評：本題主要考查了集合的包含關系判斷及其應用，屬于考查對課本中概念的理解，屬于基礎題．