已知數列
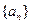
的前
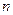
項和為
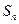
,
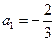
,且
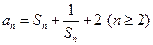
.
(1)計算
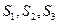
;
(2)猜想
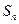
的表達式,并證明.
解:(1)
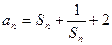
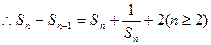
即
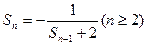
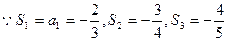
(2)猜想
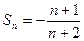
下用數學歸納法證明:
①當

命題成立,
②假設
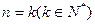
命題成立,
即
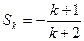
當
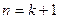
時

命題也成立
綜上:由①②得命題對一切
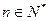
都成立。
練習冊系列答案
相關習題
科目:高中數學
來源:不詳
題型:解答題
(本小題12分)
已知數列
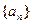
的前項和為
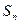
,
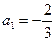
,
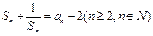
(1)求
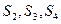
(2)猜想
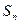
的表

達式,并用數學歸納法證明。
查看答案和解析>>
科目:高中數學
來源:不詳
題型:解答題
已知
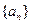
是公差不為零的等差數列,
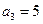
,且
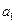
,
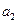
,
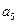
成等比數列.
(Ⅰ)求數列
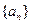
的通項公式;
(Ⅱ)若
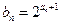
,求數列
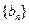
的前
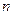
項和.
查看答案和解析>>
科目:高中數學
來源:不詳
題型:填空題
數列
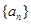
滿足
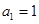
,
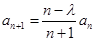
,其中
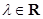
,
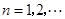
.
①當
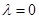
時,
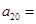
_____;
②若存在正整數
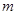
,當
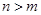
時總有
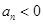
,則
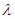
的取值范圍是_____.
查看答案和解析>>
科目:高中數學
來源:不詳
題型:單選題
數列
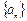
中,如果
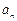
=3n(n=1,2

,3,…) ,那么這個數列是 ( )
| A.公差為2的等差數列 | B.公差為3的等差數列
 | C.首項為3的等比數列 | D.首項為1的等比數列 |
查看答案和解析>>
科目:高中數學
來源:不詳
題型:填空題
等差數列
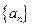
的前
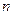
項和為
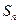
,且
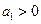
,若存在自然數
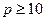
,使得
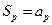
,則當
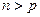
時,
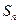
與
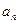
的大小關系是 。
查看答案和解析>>
主站蜘蛛池模板:
久久亚洲精品国产亚洲老地址
|
91久久综合亚洲鲁鲁五月天
|
久久精品99|
97免费在线视频
|
日韩大片免费观看视频播放
|
国产精品揄拍一区二区久久国内亚洲精
|
久久久久久毛片
|
日韩精品一区在线
|
国产精品美女久久久久久免费
|
av在线一区二区三区
|
亚洲婷婷免费
|
日一日啪一啪
|
国产一区精品视频
|
毛片网站免费观看
|
国产精品视频久久
|
日本激情视频在线播放
|
免费国产一区二区
|
欧美黄色一级
|
国产一区在线免费
|
午夜高清视频
|
亚洲成人精品在线
|
91精品国产高清一区二区三区
|
欧美成人免费
|
中文字幕亚洲天堂
|
国产女爽123视频.cno
|
中文成人无字幕乱码精品
|
丁香婷婷久久久综合精品国产
|
久久99精品久久久久久琪琪
|
日韩免费视频一区二区
|
亚洲国产精品一区二区三区
|
蜜桃精品视频在线
|
亚洲一区二区在线免费观看
|
欧美一区二区三区在线
|
久在线观看
|
日本激情视频在线观看
|
久久精品免费一区二区三区
|
欧美一区二区三区黄
|
欧美日韩福利
|
久草在线|
国产精品一区二区三区麻豆
|
久久mm|

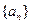 的前
的前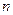 項和為
項和為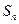 ,
,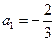 ,且
,且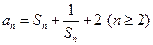 .
.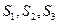 ;
;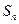 的表達式,并證明.
的表達式,并證明.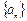 中,如果
中,如果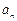 =3n(n=1,2
=3n(n=1,2 ,3,…) ,那么這個數列是 ( )
,3,…) ,那么這個數列是 ( )