
| |||||||||||||||
(1) |
解:∵平面 D(0,2,2),E(0,0,0)
|
(2) |
解:∵AD∥面BFC,
|
(3) |
解:設平面DBF的法向量為 F(0,3,0),∴ 則 取x=3,則y=2,z=1,∴ 面BCF的一個法向量為 則cos< 二面角D-BF-C的平面角為π-arccos |


科目:高中數學 來源: 題型:
 本題(1)(2)(3)三個選答題,每小題5分,請考生任選1題作答,如果多做,則按所做的前1題計分.
本題(1)(2)(3)三個選答題,每小題5分,請考生任選1題作答,如果多做,則按所做的前1題計分.| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| 2 |
| 3π |
| 4 |
| 2 |
| 3π |
| 4 |
查看答案和解析>>
科目:高中數學 來源:2004年高考教材全程總復習試卷·數學 題型:044
如圖所示,已知圓的方程是(x-1)2+y2=1,四邊形PABQ為該圓內接梯形,底邊AB為圓的直徑且在x軸上,以A,B為焦點的橢圓C過P,Q兩點.
(1)若直線QP與橢圓C的右準線相交于點M,求點M的軌跡方程;
(2)當梯形PABQ周長最大時,求橢圓C的方程.

查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 本題(1)(2)(3)三個選答題,每小題5分,請考生任選1題作答,如果多做,則按所做的前1題計分.
本題(1)(2)(3)三個選答題,每小題5分,請考生任選1題作答,如果多做,則按所做的前1題計分. ,點E,F分別為線段AB,CD的中點,則EF=________.
,點E,F分別為線段AB,CD的中點,則EF=________.查看答案和解析>>
科目:高中數學 來源:2011年陜西省西安市高三第三次質檢數學試卷(文科)(解析版) 題型:解答題
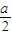 ,點E,F分別為線段AB,CD的中點,則EF= .
,點E,F分別為線段AB,CD的中點,則EF= .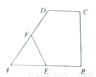
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com