Question

【題目】2018年反映社會現實的電影《我不是藥神》引起了很大的轟動，治療特種病的創新藥研發成了當務之急．為此，某藥企加大了研發投入，市場上治療一類慢性病的特效藥品的研發費用（百萬元）和銷量（萬盒）的統計數據如下：

研發費用（百萬元）	2	3	6	10	13	15	18	21
銷量（萬盒）	1	1	2	2.5	3.5	3.5	4.5	6

（1）求與的相關系數精確到0.01，并判斷與的關系是否可用線性回歸方程模型擬合？（規定：時，可用線性回歸方程模型擬合）；

（2）該藥企準備生產藥品的三類不同的劑型，，，并對其進行兩次檢測，當第一次檢測合格后，才能進行第二次檢測．第一次檢測時，三類劑型，，合格的概率分別為，，，第二次檢測時，三類劑型，，合格的概率分別為，，．兩次檢測過程相互獨立，設經過兩次檢測后，，三類劑型合格的種類數為，求的數學期望．

附：（1）相關系數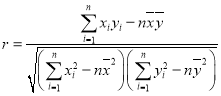

（2），，，．

Answer 1

【答案】（1）0.98;可用線性回歸模型擬合．（2）

【解析】

（1）根據題目提供的數據求出，代入相關系數公式求出，根據的大小來確定結果；

（2）求出藥品的每類劑型經過兩次檢測后合格的概率，發現它們相同，那么經過兩次檢測后，，三類劑型合格的種類數為，服從二項分布，利用二項分布的期望公式求解即可.

解：（1）由題意可知，

，

由公式，

，∴與的關系可用線性回歸模型擬合；

（2）藥品的每類劑型經過兩次檢測后合格的概率分別為

，，，

由題意， ，

.