
���}Ŀ����D����֪�E�A![]() ���ҽ��c(di��n)��
���ҽ��c(di��n)��![]() ���c(di��n)
���c(di��n)![]() �քe�ǙE�A
�քe�ǙE�A![]() ���ϡ�����c(di��n)���c(di��n)
���ϡ�����c(di��n)���c(di��n)![]() ��ֱ��
��ֱ��![]() �ϵ�һ��(g��)��(d��ng)�c(di��n)���c
�ϵ�һ��(g��)��(d��ng)�c(di��n)���c![]() �S�Ľ��c(di��n)���⣩��ֱ��
�S�Ľ��c(di��n)���⣩��ֱ��![]() ���E�A����һ��(g��)�c(di��n)
���E�A����һ��(g��)�c(di��n)![]() .
.
��1����(d��ng)ֱ��![]() ��(j��ng)�^�E�A���ҽ��c(di��n)
��(j��ng)�^�E�A���ҽ��c(di��n)![]() �r(sh��)����
�r(sh��)����![]() ����e��
����e��
��2����ӛֱ��![]() ��б�ʷքe��
��б�ʷքe��![]() �����C��
�����C��![]() �鶨ֵ��
�鶨ֵ��
����![]() ��ȡֵ����.
��ȡֵ����.
���𰸡���1��![]() ��2����Ҋ������
��2����Ҋ������![]()
��������
ԇ�}��1����(li��n)��ֱ��![]() �ķ��̞�
�ķ��̞�![]() �c�E�A����
�c�E�A����![]() �ķ��̽M��������c(di��n)
�ķ��̽M��������c(di��n)![]() ����(bi��o)
����(bi��o)![]() ���M(j��n)������c(di��n)��ֱ���ľ��x��ʽ����ϵĸ�
���M(j��n)������c(di��n)��ֱ���ľ��x��ʽ����ϵĸ�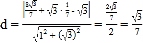 ���\(y��n)�������ε���e��ʽ��⣻��2�������б��
���\(y��n)�������ε���e��ʽ��⣻��2�������б��![]() ��ֵ����Ӌ(j��)����e�M(j��n)�����㣻���\(y��n)��ֱ���c�E�A��λ���P(gu��n)ϵӋ(j��)���������
��ֵ����Ӌ(j��)����e�M(j��n)�����㣻���\(y��n)��ֱ���c�E�A��λ���P(gu��n)ϵӋ(j��)���������![]() ������(bi��o)��ʽ�����\(y��n)�������Ĕ�(sh��)���e��ʽ�M(j��n)�����C��
������(bi��o)��ʽ�����\(y��n)�������Ĕ�(sh��)���e��ʽ�M(j��n)�����C��
�⣺��1�����}��![]() �����c(di��n)
�����c(di��n)![]() ��
��
��(d��ng)ֱ��![]() �^�E�A���ҽ��c(di��n)
�^�E�A���ҽ��c(di��n)![]() �r(sh��)���tֱ��
�r(sh��)���tֱ��![]() �ķ��̞�
�ķ��̞�![]() ����
����![]() ��
��
(li��n)��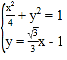 �����
�����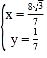 ��
��![]() (�ᣩ����
(�ᣩ����![]() .
.
�B![]() ���tֱ��
���tֱ��![]() ����
���� ![]() ��
��
��![]() ��
��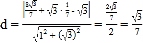 .
.
��![]() .
.
��2����:��һ�����O(sh��)![]() ����
����![]() ���tֱ��
���tֱ��![]() ��б�ʞ�
��б�ʞ�![]() ��
��
�tֱ��![]() �ķ��̞�
�ķ��̞�![]() ��
��
(li��n)��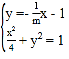 ����(ji��n)��
����(ji��n)��![]() ��
��
���![]() ��
��
����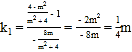 ��
��![]() ��
��
����![]() �鶨ֵ.
�鶨ֵ.
���ɢ�֪��![]() ��
��![]() ��
��
����![]() ��
��
��![]()
��![]() ��
��
��?y��n)?/span>![]() ��
��![]() �φ��{(di��o)�f����
�φ��{(di��o)�f����
����![]() ����
����![]() ��ȡֵ������
��ȡֵ������![]() .
.
�ⷨ�������O(sh��)�c(di��n)![]() ���tֱ��
���tֱ��![]() �ķ��̞�
�ķ��̞�![]() ��
��
��![]() ����
����![]() .
.
����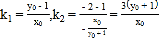 ��
��
����![]() (��ֵ��.
(��ֵ��.
���ɢ�֪��![]() ��
��![]() ��
��
���ԣ�![]()
![]() .
.
��![]() ���t
���t![]() ��
��
��?y��n)?/span>![]() ��
��![]() �φ��{(di��o)�f�p,
�φ��{(di��o)�f�p,
����![]() ����
����![]() ��ȡֵ������
��ȡֵ������![]() .
.


 ��x��܇ϵ�д�
��x��܇ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���������F![]() �У�����
�У�����![]() ����Σ�
����Σ�![]() ƽ��
ƽ��![]() ��
��![]() �����c(di��n)
�����c(di��n)
��1���C����![]() ƽ��
ƽ��![]() ��
��
��2���C����![]() ƽ��
ƽ��![]() ��
��
��3����![]() �����F
�����F![]() ���w�e��
���w�e��![]() �����c(di��n)D��ƽ��
�����c(di��n)D��ƽ��![]() �ľ��x.
�ľ��x.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ������D��ʾ�Ď��w�У���߅��![]() ��ƽ����߅�Σ�
��ƽ����߅�Σ�![]() ��
��![]() ƽ��
ƽ��![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() �����c(di��n).
�����c(di��n).
���������C��![]() ƽ��
ƽ��![]() ��
��
������������![]() �Ĵ�С��
�Ĵ�С��
�������ھ���![]() ���Ƿ����һ�c(di��n)
���Ƿ����һ�c(di��n)![]() ��ʹ��
��ʹ��![]() �c
�c![]() ���ɵĽǞ�
���ɵĽǞ�![]() �� �����ڣ����
�� �����ڣ����![]() ���L(zh��ng)�ȣ��������ڣ�Ո(q��ng)�f������.
���L(zh��ng)�ȣ��������ڣ�Ո(q��ng)�f������.

�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D��ʾ����ƽ��ֱ������(bi��o)ϵ![]() �У���֪�E�A
�У���֪�E�A![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ��
��![]() ��
��![]() �ǙE�A�ϵ��Ă�(g��)��(d��ng)�c(di��n)����
�ǙE�A�ϵ��Ă�(g��)��(d��ng)�c(di��n)����![]() ��
��![]() ������
������![]() �c
�c![]() ���ڙE�A
���ڙE�A![]() ��(n��i)һ�c(di��n)
��(n��i)һ�c(di��n)![]() .��(d��ng)�c(di��n)
.��(d��ng)�c(di��n)![]() ������(bi��o)��
������(bi��o)��![]() ����
����![]() ��
��![]() �քe��E�A
�քe��E�A![]() ������c(di��n)������c(di��n)�غϕr(sh��)����߅��
������c(di��n)������c(di��n)�غϕr(sh��)����߅��![]() ����e��4.
����e��4.
������E�A![]() �Ę�(bi��o)��(zh��n)���̣�
�Ę�(bi��o)��(zh��n)���̣�
�����C������(d��ng)�c(di��n)![]() ��
��![]() ��
��![]() ��
��![]() �ڙE�A���\(y��n)��(d��ng)�r(sh��)��
�ڙE�A���\(y��n)��(d��ng)�r(sh��)��![]() ��
��![]() ���Ƕ�ֵ.
���Ƕ�ֵ.

�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����ƽ��ֱ������(bi��o)ϵ![]() �У�ֱ��
�У�ֱ��![]() �ą���(sh��)���̞飺
�ą���(sh��)���̞飺![]() ��
��![]() �酢��(sh��)��
�酢��(sh��)��![]() ������
������![]() ��O�c(di��n)��
��O�c(di��n)��![]() �S�������S��O�S�������O����(bi��o)ϵ������
�S�������S��O�S�������O����(bi��o)ϵ������![]() �ĘO����(bi��o)���̞�
�ĘO����(bi��o)���̞�![]() .
.
��1����(d��ng)![]() �r(sh��)������ֱ��
�r(sh��)������ֱ��![]() ����ͨ���̺�����
����ͨ���̺�����![]() ��ֱ������(bi��o)���̣�
��ֱ������(bi��o)���̣�
��2�����c(di��n)![]() ���O(sh��)����
���O(sh��)����![]() �cֱ��
�cֱ��![]() �����c(di��n)
�����c(di��n)![]() ����
����![]() ����Сֵ.
����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����ָͨ��(sh��)�ǽ�ͨ����ָ��(sh��)�ĺ�(ji��n)�Q���ǾC�Ϸ�ӳ��·�W(w��ng)��ͨ����µĸ��ӛ��ָͨ��(sh��)��T.�䷶����[0��10]���քe���傀(g��)��(j��)�e��T��[0��2����ͨ��T��[2��4��������ͨ��T��[4��6���p�ȓ��£�T��[6��8���жȓ��£�T��[8��10]��(y��n)��?f��)��£����߷�r(sh��)�Σ�T��2������ij�н�ָͨ�]�����xȡ���Ѕ^(q��)20��(g��)��ͨ·�Σ�����(j��)�佻ָͨ��(sh��)��(sh��)��(j��)�L�ƵIJ���ֱ���D��D��ʾ.
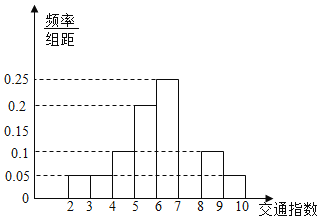
��1��Ո(q��ng)�a(b��)ȫֱ���D��������p�ȓ��¡��жȓ��¡���(y��n)��?f��)���·�θ��ж��ق�(g��)��
��2���÷ӳ�ӵķ����Ľ�ָͨ��(sh��)��[4��6����[6��8����[8��l0]��·���й���ȡ6��(g��)·�Σ������γ�ȡ������(g��)��(j��)�e·�εĂ�(g��)��(sh��)��
��3���ģ�2���г����6��(g��)·������ȡ2��(g��)��������һ��(g��)·�Ξ��p�ȓ��µĸ���.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����C1�ą���(sh��)���̞�![]() ��t�酢��(sh��)����������(bi��o)ԭ�c(di��n)��O�c(di��n)��x�S�������S��O�S�����O����(bi��o)ϵ������C2�ĘO����(bi��o)���̞��=2cos�ȣ�
��t�酢��(sh��)����������(bi��o)ԭ�c(di��n)��O�c(di��n)��x�S�������S��O�S�����O����(bi��o)ϵ������C2�ĘO����(bi��o)���̞��=2cos�ȣ�
��1����C1�ą���(sh��)���̻���O����(bi��o)���̣�
��2����C1�cC2���c(di��n)�ĘO����(bi��o)���ѡ�0��0�ܦȣ�2�У���
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
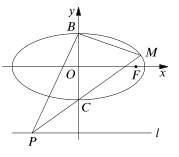
���}Ŀ����D����������![]() �У�
��![]() ����
����![]() ,
,![]() ,
,![]() ,
,![]() .
.

��1���C��![]() ;
;
��2������ֱ��![]() ��
��![]() ���ɽǵ�����ֵ;
���ɽǵ�����ֵ;
��3��������![]() ��ƽ��ǵ�����ֵ.
��ƽ��ǵ�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���������}���������}�Ă�(g��)��(sh��)�ǣ� ��
��1����ֱ��ͬһ�lֱ���ăɗlֱ������ƽ��
��2���cͬһ��(g��)ƽ��A����ȵăɗlֱ������ƽ��
��3��ƽ����ͬһ��(g��)ƽ��ăɗlֱ������ƽ��
��4���ɗlֱ���ܴ_��һ��(g��)ƽ��
��5����ֱ��ͬһ��(g��)ƽ��ăɂ�(g��)ƽ��ƽ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com