
【題目】定義:如果函數f(x)在[a,b]上存在x1 , x2(a<x1<x2<b)滿足 ![]() ,
, ![]() ,則稱函數f(x)是[a,b]上的“雙中值函數”.已知函數f(x)=x3﹣x2+a是[0,a]上的“雙中值函數”,則實數a的取值范圍是( )
,則稱函數f(x)是[a,b]上的“雙中值函數”.已知函數f(x)=x3﹣x2+a是[0,a]上的“雙中值函數”,則實數a的取值范圍是( )
A.![]()
B.( ![]() )
)
C.( ![]() ,1)
,1)
D.( ![]() ,1)
,1)
科目:高中數學 來源: 題型:
【題目】如圖![]() ,在直角梯形
,在直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,點
,點![]() 是
是![]() 邊的中點,將
邊的中點,將![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() ,連接
,連接![]() ,
, ![]() ,
, ![]() ,得到如圖
,得到如圖![]() 所示的幾何體.
所示的幾何體.
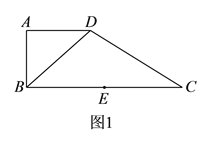
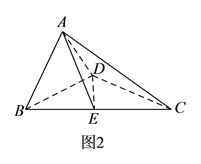
(Ⅰ)求證: ![]() 平面
平面![]() .
.
(Ⅱ)若![]() ,
, ![]() 與其在平面
與其在平面![]() 內的正投影所成角的正切值為
內的正投影所成角的正切值為![]() ,求點
,求點![]() 到平面
到平面![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知△ABC的頂點A(5,1),AB邊上的中線CM所在的直線方程為2x﹣y﹣5=0,AC邊上的高BH所在直線的方程為x﹣2y﹣5=0.
(1)求直線BC的方程;
(2)求直線BC關于CM的對稱直線方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在正方體ABCD﹣A1B1C1D1中,異面直線AD1與BD所成的角為;若AB的中點為M,DD1的中點為N,則異面直線B1M與CN所成的角為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,斜三棱柱ABC﹣A1B1C1的所有棱長均為a,M是BC的中點,側面B1C1CB⊥底面ABC,且AC1⊥BC.
(Ⅰ)求證:BC⊥C1M;
(Ⅱ)求二面角A1﹣AB﹣C的平面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知a,b是正實數,設函數f(x)=xlnx,g(x)=﹣a+xlnb.
(Ⅰ)設h(x)=f(x)﹣g(x),求h(x)的單調區間;
(Ⅱ)若存在x0 , 使x0∈[ ![]() ,
, ![]() ]且f(x0)≤g(x0)成立,求
]且f(x0)≤g(x0)成立,求 ![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知二次函數f(x)=mx2﹣2x﹣3,關于實數x的不等式f(x)≤0的解集為(﹣1,n)
(1)當a>0時,解關于x的不等式:ax2+n+1>(m+1)x+2ax;
(2)是否存在實數a∈(0,1),使得關于x的函數y=f(ax)﹣3ax+1(x∈[1,2])的最小值為﹣5?若存在,求實數a的值;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com