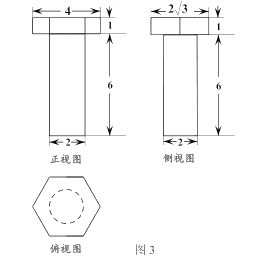
【題目】如圖是一種螺栓的簡易三視圖,其螺帽俯視圖是一個正六邊形,則由三視圖尺寸,該螺栓的表面積為( )
A. 
B. 
C. 
D. 
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】
世紀
年代，里克特（C.F.Richter）制定了一種表明地震能量大小的尺度，就是使用測震儀衡量地震能量的等級，地震能量越大，測震儀記錄的地震曲線的振幅就越大.這就是我們常說的里氏震級
，其計算公式為：
，其中，
是被測地震的最大振幅，
是“標準地震”的振幅（使用標準地震振幅是為了修正測震儀距實際震中的距離造成的偏差）.（以下數據供參考：
，
，
）
（1）根據中國地震臺網測定，
年
月
日
時
分，新疆巴音郭楞蒙古自治州若羌縣發生地震，一個距離震中
千米的測震儀記錄的地震最大振幅是，此時標準地震的振幅是
，計算這次地震的震級（精確到
）；
（2）
年
月
日
時
分
秒在我國四川省汶川地區發生特大地震，根據中華人民共和國地震局的數據，此次地震的里氏震級達
，地震烈度達到
度.此次地震的地震波已確認共環繞了地球
圈.地震波及大半個中國及亞洲多個國家和地區，北至遼寧，東至上海，南至香港、澳門、泰國、越南，西至巴基斯坦均有震感.請計算汶川地震的最大振幅是
級地震的最大振幅的多少倍？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某學校要定制高一年級的校服，學生根據廠家提供的參考身高選擇校服規格.據統計，高一年級女生需要不同規格校服的頻數如表所示.
校服規格 | 155 | 160 | 165 | 170 | 175 | 合計 |
頻數 | 39 | 64 | 167 | 90 | 26 | 386 |
如果用一個量來代表該校高一年級女生所需校服的規格，那么在中位數、平均數和眾數中，哪個量比較合適？試討論用表中的數據估計全國高一年級女生校服規格的合理性.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】我國是世界嚴重缺水的國家，城市缺水問題較為突出，某市政府為了鼓勵居民節約用水，計劃在本市試行居民生活用水定額管理，即確定一個合理的居民月用水量標準
（噸），用水量不超過的部分按平價收費，超過的部分按議價收費，為了了解全市民月用水量的分布情況，通過抽樣，獲得了100位居民某年的月用水量（單位：噸），將數據按照
分成9組，制成了如圖所示的頻率分布直方圖.
（Ⅰ）求直方圖中的
值；
（Ⅱ）已知平價收費標準為
元/噸，議價收費標準為
元/噸，當
時，估計該市居民的月平均水費.（同一組中的數據用該組區間的中點值代替）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】我國是世界嚴重缺水的國家，城市缺水問題較為突出，某市政府為了鼓勵居民節約用水，計劃在本市試行居民生活用水定額管理，即確定一個合理的居民月用水量標準
（噸），用水量不超過的部分按平價收費，超過的部分按議價收費，為了了解全市民月用水量的分布情況，通過抽樣，獲得了100位居民某年的月用水量（單位：噸），將數據按照
分成9組，制成了如圖所示的頻率分布直方圖.
（Ⅰ）若全市居民中月均用水量不低于3噸的人數為3.6萬，試估計全市有多少居民？并說明理由；
（Ⅱ）若該市政府擬采取分層抽樣的方法在用水量噸數為
和
之間選取7戶居民作為議價水費價格聽證會的代表，并決定會后從這7戶家庭中按抽簽方式選出4戶頒發“低碳環保家庭”獎，設
為用水量噸數在中的獲獎的家庭數，
為用水量噸數在中的獲獎家庭數，記隨機變量
，求
的分布列和數學期望．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某單位有2000名職工，老年、中年、青年分布在管理、技術開發、營銷、生產各部門中，如下表所示：
人數 | 管理 | 技術開發 | 營銷 | 生產 | 共計 |
老年 | 40 | 40 | 40 | 80 | 200 |
中年 | 80 | 120 | 160 | 240 | 600 |
青年 | 40 | 160 | 280 | 720 | 1 200 |
小計 | 160 | 320 | 480 | 1 040 | 2 000 |
(1)若要抽取40人調查身體狀況，則應怎樣抽樣？
(2)若要開一個25人的討論單位發展與薪金調整方面的座談會，則應怎樣抽選出席人？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】若函數y=f（x）在區間D上是增函數，且函數y=
在區間D上是減函數，則稱函數f（x）是區間D上的“H函數”．對于命題：
①函數f（x）=-x+
是區間（0，1）上的“H函數”；
②函數g（x）=
是區間（0，1）上的“H函數”．下列判斷正確的是（ ）
A. 
和
均為真命題 B. 為真命題，為假命題
C. 為假命題，為真命題 D. 和均為假命題
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了了解某地區高三學生的身體發育情況，抽查了該地區100名年齡為17.5歲～１８歲的男生體重(kg)，得到頻率分布直方圖如下：求：
（1）根據直方圖可得這100名學生中體重在(56，64)的學生人數.
（2）請根據上面的頻率分布直方圖估計該地區17.5-18歲的男生體重.
（3）若在這100名男生中隨意抽取1人，該生體重低于62的概率是多少？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
