
已知函數 .
.
(Ⅰ)當 時,求曲線
時,求曲線 在原點處的切線方程;
在原點處的切線方程;
(Ⅱ)當 時,討論函數
時,討論函數 在區間
在區間 上的單調性;
上的單調性;
(Ⅲ)證明不等式 對任意
對任意 成立.
成立.
(Ⅰ) .
.
(Ⅱ)函數 在區間
在區間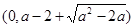 單調遞減,在區間
單調遞減,在區間 上單調遞增.
上單調遞增.
(Ⅲ)由(Ⅱ)知,當 時,
時,  在區間
在區間 上單調遞增;
上單調遞增;
從而可得 ,
,
得到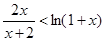 對任意
對任意 成立.
成立.
通過取 ,
, ,得
,得 ,
, .
.
將上述n個不等式求和,得到: ,
,
證得 對任意
對任意 成立.
成立.
【解析】
試題分析:(Ⅰ)首先求 ,切線的斜率
,切線的斜率 ,求得切線方程.
,求得切線方程.
(Ⅱ)當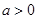 時,根據
時,根據 ,只要考查
,只要考查 的分子
的分子 的符號.
的符號.
通過討論 ,得
,得 時
時 在區間
在區間 上單調遞增;
上單調遞增;
當 時,令
時,令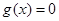 求得其根
求得其根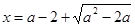 . 利用“表解法”得出結論:函數
. 利用“表解法”得出結論:函數 在區間
在區間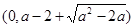 單調遞減,在區間
單調遞減,在區間 上單調遞增.
上單調遞增.
(Ⅲ)由(Ⅱ)知,當 時,
時,  在區間
在區間 上單調遞增;
上單調遞增;
從而可得 ,
,
得到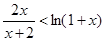 對任意
對任意 成立.
成立.
通過取 ,
, ,得
,得 ,
, .
.
將上述n個不等式求和,得到: ,
,
證得 對任意
對任意 成立.
成立.
試題解析:
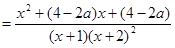 .
.
(Ⅰ)當 時,
時,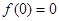 ,切線的斜率
,切線的斜率 ,
,
所以切線方程為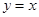 ,即
,即 .
3分
.
3分
(Ⅱ)當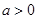 時,因為
時,因為 ,所以只要考查
,所以只要考查 的符號.
的符號.
由 ,得
,得 ,
,
當 時,
時, ,從而
,從而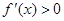 ,
, 在區間
在區間 上單調遞增;
上單調遞增;
當 時,由
時,由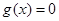 解得
解得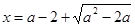 . 6分
. 6分
當 變化時,
變化時, 與
與 的變化情況如下表:
的變化情況如下表:
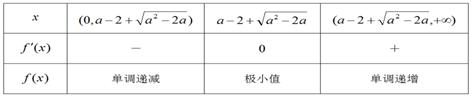
函數 在區間
在區間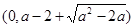 單調遞減,在區間
單調遞減,在區間 上單調遞增. 9分
上單調遞增. 9分
(Ⅲ)由(Ⅱ)知,當 時,
時,  在區間
在區間 上單調遞增;
上單調遞增;
所以 ,
,
即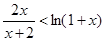 對任意
對任意 成立.
11分
成立.
11分
取 ,
, ,
,
得 ,即
,即 ,
, . 13分
. 13分
將上述n個不等式求和,得到: ,
,
即不等式 對任意
對任意 成立.
14分
成立.
14分
考點:1、導數的幾何意義,2、應用導數研究函數的單調性、3、證明不等式.


 期末沖刺100分創新金卷完全試卷系列答案
期末沖刺100分創新金卷完全試卷系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com