
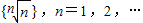 ,則數列中最大項的值為 .
,則數列中最大項的值為 . 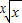 ,(x>0),則lny=
,(x>0),則lny= lnx,再設F(x)=lny=
lnx,再設F(x)=lny=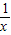 lnx,求導數F′(x)=-
lnx,求導數F′(x)=-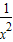 lnx+
lnx+ =
=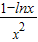 ,利用導數研究它的單調性,得出F(x)在區間[3,+∞)是減函數,在(0,2]是增函數,又由于
,利用導數研究它的單調性,得出F(x)在區間[3,+∞)是減函數,在(0,2]是增函數,又由于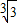 >
>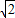 ,從而得出數列中最大項的值.
,從而得出數列中最大項的值.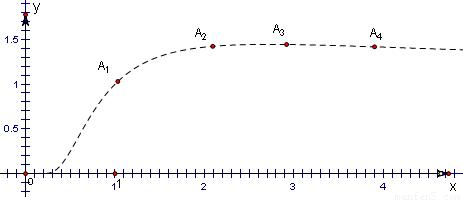 解:設y=
解:設y=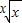 ,(x>0),
,(x>0),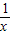 lnx,
lnx,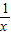 lnx,
lnx, lnx+
lnx+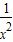 =
=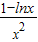 ,
,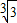 >
>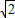 ,
,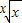 的最大值為
的最大值為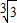 .
. .
.

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com