分析:(1)由于圓O:x
2+y
2=4的圓心為( 0,0),半徑等于2,顯然有一條切線為x=2.當切線的斜率存在時,用點斜式設出直線方程,根據圓心到切線的距離d=半徑r,求出斜率的值,
即可求得圓的切線方程.
(2)由題意可得,直線l的斜率存在,用點斜式設出直線方程,根據圓心到切線的距離d=
=
,求出斜率的值,即可求得直線l的方程.
解答:解:(1)由于圓O:x
2+y
2=4的圓心為( 0,0),半徑等于2,顯然有一條切線為x=2.
當切線的斜率存在時,∵點P(2,4)不在圓O上,
∴切線PT的直線方程可設為y=k(x-2)+4,
根據圓心到切線的距離d=半徑r,
∴
=2,解得
k=,所以圓的切線方程為
y=(x-2)+4,即3x-4y+10=0,
綜上可得,圓的切線方程為3x-4y+10=0 或x=2.
(2)由題意可得,直線l的斜率存在,設直線l的方程為 y=k(x-2)+4,即 kx-y+4-2k=0.
由弦長公式可得圓心到直線l的距離為 d=
=
,即
=
,解得 k=1,或 k=7.
故直線l的方程為 y=x+2,或y=7x-10,即 x-y+2=0,或 7x-y-10=0.
點評:本題主要考查直線和圓的位置關系,點到直線的距離公式,弦長公式的應用,屬于中檔題.



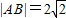 ,求直線l的方程.
,求直線l的方程. .
. ,求直線l的方程.
,求直線l的方程.