
 已知,f(x)=xlnx,g(x)=ax2+bx-1,函數y=g(x)的導數g′(x)的圖象如圖所示.
已知,f(x)=xlnx,g(x)=ax2+bx-1,函數y=g(x)的導數g′(x)的圖象如圖所示.| 1 |
| 2 |
| 1 |
| x |
| 1-x |
| x |
2(x-
| ||
| 2x2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| x | (0,x0) | x0 | (x0,1) | 1 | (1,+∞) |
| h'(x) | - | 0 | + | 0 | - |
| h(x) | ↘ | 極小值 | ↗ | 極大值1 | ↘ |
| x | 2 0 |
| x | 2 0 |
| x | 2 0 |
| 1 |
| 2 |
| 3 |
| 4 |


 活力課時同步練習冊系列答案
活力課時同步練習冊系列答案 學業測評一課一測系列答案
學業測評一課一測系列答案科目:高中數學 來源: 題型:
| y1-y2 | x1-x2 |
查看答案和解析>>
科目:高中數學 來源: 題型:044
已知函數f(x)=x2-1(x≥1)的圖象為 C1,曲線C2與C1關于直線y=x對稱。
(1)求曲線C2的方程y=g(x);
(2)設函數y=g(x)的定義域為M,xl,x2∈ M,且xl≠x2,求證|g(x1)-g(x2)|<|x1-x2|;
(3)設A,B為曲線C2上任意不同兩點,證明直線AB與直線y=x必相交。
查看答案和解析>>
科目:高中數學 來源:數學教研室 題型:044
(1)求曲線C2的方程y=g(x);
(2)設函數y=g(x)的定義域為M,xl,x2∈ M,且xl≠x2,求證|g(x1)-g(x2)|<|x1-x2|;
(3)設A,B為曲線C2上任意不同兩點,證明直線AB與直線y=x必相交。
查看答案和解析>>
科目:高中數學 來源:2012-2013學年廣東省深圳市高三第一次調研考試理科數學試卷(解析版) 題型:選擇題
函數y=f(x),x∈D,若存在常數C,對任意的xl∈D,仔在唯一的x2∈D,使得 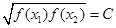 ,則稱函數f(x)在D上的幾何平均數為C.已知f(x)=x3,x∈[1,2],則函數f(x)=x3在[1,2]上的幾何平均數為
,則稱函數f(x)在D上的幾何平均數為C.已知f(x)=x3,x∈[1,2],則函數f(x)=x3在[1,2]上的幾何平均數為
A.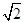 B.2 C.4
D. 2
B.2 C.4
D. 2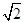
查看答案和解析>>
科目:高中數學 來源:2011-2012學年安徽省淮北市高三第一次模擬考試文科數學 題型:解答題
.(本題滿分13分)設函數 ,方程f(x)=x有唯一的解,
,方程f(x)=x有唯一的解,
已知f(xn)=xn+1(n∈N﹡)且f(xl)= .
.
(1)求證:數列{ )是等差數列;
)是等差數列;
(2)若 ,求Sn=b1+b2+b3+…+bn
,求Sn=b1+b2+b3+…+bn
(3)在(2)的條件下,是否存在最小正整數m,使得對任意n∈N﹡,有 成立,若存在,求出m的值;若不存在,請說明理由。
成立,若存在,求出m的值;若不存在,請說明理由。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com