
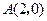 ,
,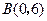 ,
,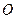 為原點.
為原點.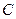 在線段
在線段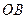 上,且
上,且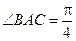 ,求
,求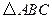 的面積;
的面積;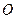 關于直線
關于直線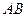 的對稱點為
的對稱點為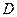 ,延長
,延長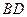 到
到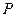 ,且
,且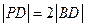 ,已知直線
,已知直線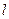 :
: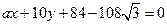 經過點
經過點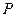 ,求直線
,求直線 的傾斜角.
的傾斜角. 浙江名校名師金卷系列答案
浙江名校名師金卷系列答案科目:高中數(shù)學 來源:不詳 題型:解答題
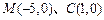 ,
,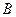 分
分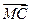 所成的比為2,
所成的比為2,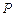 是平面上一動點,且滿足
是平面上一動點,且滿足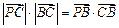 .(1)求點
.(1)求點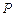 的軌跡
的軌跡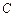 對應的方程;(2) 已知點
對應的方程;(2) 已知點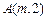 在曲線
在曲線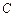 上,過點
上,過點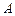 作曲線
作曲線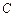 的兩條弦
的兩條弦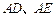 ,且直線
,且直線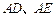 的斜率
的斜率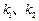 滿足
滿足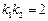 ,試推斷:動直線
,試推斷:動直線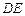 有何變化規(guī)律,證明你的結論.
有何變化規(guī)律,證明你的結論.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:填空題
 )、N(-4,-
)、N(-4,- ),給出下列曲線方程:
),給出下列曲線方程: 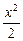 +y2="1," ④
+y2="1," ④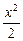 -y2=1,在曲線上存在點P滿足|MP|=|NP|的所有曲線方程是_________.
-y2=1,在曲線上存在點P滿足|MP|=|NP|的所有曲線方程是_________. 查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com