
【題目】已知![]() ,
,![]() 是曲線
是曲線![]() 上任意一點,動點
上任意一點,動點![]() 滿足
滿足![]() .
.
(1)求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)過點![]() 的直線交
的直線交![]() 于
于![]() ,
,![]() 兩點,過原點
兩點,過原點![]() 與點
與點![]() 的直線交直線
的直線交直線![]() 于點
于點![]() ,求證:
,求證:![]() .
.
【答案】(1)![]() ;(2)詳見解析.
;(2)詳見解析.
【解析】
(1)設(shè)![]() ,
,![]() ,由
,由![]() 推出
推出 代入方程即可求解點
代入方程即可求解點![]() 的軌跡
的軌跡![]() 的方程;(2)直線
的方程;(2)直線![]() 的斜率存在,其方程可設(shè)為
的斜率存在,其方程可設(shè)為![]() ,設(shè)
,設(shè)![]() ,
,![]() ,聯(lián)立
,聯(lián)立![]() ,利用韋達定理,轉(zhuǎn)化求解斜率,推出結(jié)果即可.
,利用韋達定理,轉(zhuǎn)化求解斜率,推出結(jié)果即可.
解:(1)設(shè)![]() ,
,![]() ,由
,由![]() 得:
得:![]() ,
,
則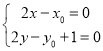 ,
,
即 ,
,
因為點![]() B為曲線
B為曲線![]() 上任意一點,故
上任意一點,故![]() ,代入得
,代入得![]() .
.
所以點![]() 的軌跡
的軌跡![]() 的方程是
的方程是![]() .
.
(2)依題意得,直線![]() 的斜率存在,其方程可設(shè)為
的斜率存在,其方程可設(shè)為![]() ,
,
設(shè)![]() ,
,![]() ,
,
聯(lián)立![]() 得
得![]() ,
,
所以![]() ,
,![]() .
.
因為直線![]() 的方程為
的方程為![]() ,
,
且![]() 是直線
是直線![]() 與直線
與直線![]() 的交點,所以
的交點,所以![]() 的坐標(biāo)為
的坐標(biāo)為![]() .
.
根據(jù)拋物線的定義![]() 等于點
等于點![]() 到準(zhǔn)線
到準(zhǔn)線![]() 的距離,由于
的距離,由于![]() 在準(zhǔn)線
在準(zhǔn)線![]() 上,
上,
所以要證明![]() ,只需證明
,只需證明![]() 垂直準(zhǔn)線
垂直準(zhǔn)線![]() ,
,
即證![]() 軸.
軸.
因為![]() 的縱坐標(biāo)
的縱坐標(biāo)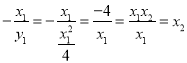 .
.
所以![]() 軸成立,所以
軸成立,所以![]() 成立.
成立.


 課時掌控隨堂練習(xí)系列答案
課時掌控隨堂練習(xí)系列答案 一課一練一本通系列答案
一課一練一本通系列答案 浙江之星學(xué)業(yè)水平測試系列答案
浙江之星學(xué)業(yè)水平測試系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知如圖,矩形![]() 所在平面與底面
所在平面與底面![]() 垂直,在直角梯形
垂直,在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() .
.
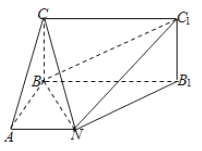
(1)求證:![]() 平面
平面![]() ;
;
(2)求證:![]() 平面
平面![]() ;
;
(3)求![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知P是圓F1:(x+1)2+y2=16上任意一點,F2(1,0),線段PF2的垂直平分線與半徑PF1交于點Q,當(dāng)點P在圓F1上運動時,記點Q的軌跡為曲線C.
(1)求曲線C的方程;
(2)記曲線C與x軸交于A,B兩點,M是直線x=1上任意一點,直線MA,MB與曲線C的另一個交點分別為D,E,求證:直線DE過定點H(4,0).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】從某部門參加職業(yè)技能測試的2000名員工中抽取100名員工,將其成績(滿分100分)按照![]() ,
,![]() ,
,![]() ,
,![]() 分成4組,得到如圖所示的頻率分布直方圖.
分成4組,得到如圖所示的頻率分布直方圖.
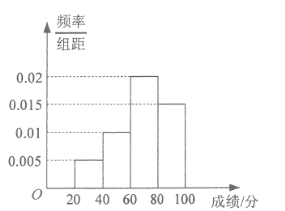
(1)估計該部門參加測試員工的成績的中位數(shù);
(2)估計該部門參加測試員工的平均成績.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某鮮花店每天制作![]() 、
、![]() 兩種鮮花共
兩種鮮花共![]() 束,每束鮮花的成本為
束,每束鮮花的成本為![]() 元,售價
元,售價![]() 元,如果當(dāng)天賣不完,剩下的鮮花作廢品處理.該鮮花店發(fā)現(xiàn)這兩種鮮花每天都有剩余,為此整理了過往100天這兩種鮮花的日銷量(單位:束),得到如下統(tǒng)計數(shù)據(jù):
元,如果當(dāng)天賣不完,剩下的鮮花作廢品處理.該鮮花店發(fā)現(xiàn)這兩種鮮花每天都有剩余,為此整理了過往100天這兩種鮮花的日銷量(單位:束),得到如下統(tǒng)計數(shù)據(jù):
| 48 | 49 | 50 | 51 |
天數(shù) | 25 | 35 | 20 | 20 |
| 48 | 49 | 50 | 51 |
天數(shù) | 40 | 35 | 15 | 10 |
以這100天記錄的各銷量的頻率作為各銷量的概率,假設(shè)這兩種鮮花的日銷量相互獨立.
(1)記該店這兩種鮮花每日的總銷量為![]() 束,求
束,求![]() 的分布列.
的分布列.
(2)鮮花店為了減少浪費,提升利潤,決定調(diào)查每天制作鮮花的量![]() 束.以銷售這兩種鮮花的日總利潤的期望值為決策依據(jù),在每天所制鮮花能全部賣完與
束.以銷售這兩種鮮花的日總利潤的期望值為決策依據(jù),在每天所制鮮花能全部賣完與![]() 之中選其一,應(yīng)選哪個?
之中選其一,應(yīng)選哪個?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】函數(shù)![]() ,其中
,其中![]() ,
,![]() ,為實常數(shù)
,為實常數(shù)
(1)若![]() 時,討論函數(shù)
時,討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(2)若![]() 時,不等式
時,不等式![]() 在
在![]() 上恒成立,求實數(shù)
上恒成立,求實數(shù)![]() 的取值范圍;
的取值范圍;
(3)若![]() ,當(dāng)
,當(dāng)![]() 時,證明:
時,證明:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的焦距為4,且過點
的焦距為4,且過點![]() .
.
(1)求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
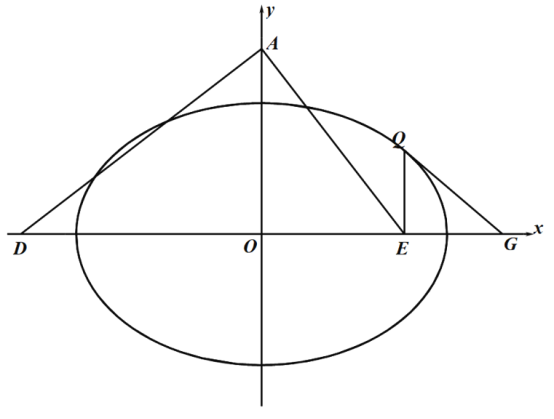
(2)設(shè)![]() 為橢圓
為橢圓![]() 上一點,過點
上一點,過點![]() 作
作![]() 軸的垂線,垂足為
軸的垂線,垂足為![]() ,取點
,取點![]() ,連接
,連接![]() ,過點
,過點![]() 作
作![]() 的垂線交
的垂線交![]() 軸于點
軸于點![]() ,點
,點![]() 是點
是點![]() 關(guān)于
關(guān)于![]() 軸的對稱點,作直線
軸的對稱點,作直線![]() ,問這樣作出的直線
,問這樣作出的直線![]() 是否與橢圓
是否與橢圓![]() 一定有唯一的公共點?并說明理由.
一定有唯一的公共點?并說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() 在點
在點![]() 處的切線方程為
處的切線方程為![]() .
.
(1)若函數(shù)![]() 存在單調(diào)遞減區(qū)間,求實數(shù)
存在單調(diào)遞減區(qū)間,求實數(shù)![]() 的取值范圍;
的取值范圍;
(2)設(shè)![]() ,對于
,對于![]() ,
,![]() 的值域為
的值域為![]() ,若
,若![]() ,求實數(shù)
,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com