
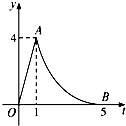
 我市沿海某醫藥研究所開發一種新藥,如果成年人按規定的劑量服用,據監測,服藥后每毫升血液中的含藥量y(微克)與時間t(小時)之間近似滿足如圖所示的曲線(OA為線段,AB為某二次函數圖象的一部分,B是拋物線頂點,O為原點).
我市沿海某醫藥研究所開發一種新藥,如果成年人按規定的劑量服用,據監測,服藥后每毫升血液中的含藥量y(微克)與時間t(小時)之間近似滿足如圖所示的曲線(OA為線段,AB為某二次函數圖象的一部分,B是拋物線頂點,O為原點). 微克時,對治療有效,求服藥一次治療疾病有效的時間.
微克時,對治療有效,求服藥一次治療疾病有效的時間.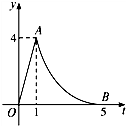
 ,解得m=-5,n=0,a=
,解得m=-5,n=0,a= .
. .
. …
…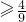 ,解得
,解得 ;
;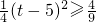 ,解得t≥
,解得t≥ ,或t≤
,或t≤ ,∴1<t
,∴1<t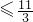 ,
,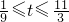 ,
,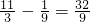 .
. 小時.
小時.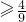 ,當1<t≤5時,
,當1<t≤5時,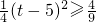 ,由此能求出服藥一次治療疾病的有效時間.
,由此能求出服藥一次治療疾病的有效時間.

 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
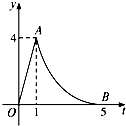
 我市沿海某醫藥研究所開發一種新藥,如果成年人按規定的劑量服用,據監測,服藥后每毫升血液中的含藥量y(微克)與時間t(小時)之間近似滿足如圖所示的曲線(OA為線段,AB為某二次函數圖象的一部分,B是拋物線頂點,O為原點).
我市沿海某醫藥研究所開發一種新藥,如果成年人按規定的劑量服用,據監測,服藥后每毫升血液中的含藥量y(微克)與時間t(小時)之間近似滿足如圖所示的曲線(OA為線段,AB為某二次函數圖象的一部分,B是拋物線頂點,O為原點).| 4 | 9 |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
| 4 |
| 9 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com