
三人獨立破譯同一份密碼.已知三人各自破譯出密碼的概率分別為![]() 且他們是否破譯出密碼互不影響.
且他們是否破譯出密碼互不影響.
(Ⅰ)求恰有二人破譯出密碼的概率;
(Ⅱ)“密碼被破譯”與“密碼未被破譯”的概率哪個大?說明理由.
解:記“第i個人破譯出密碼”為事件Ai(i=1,2,3),依題意有
![]() 且A1,A2,A3相互獨立.
且A1,A2,A3相互獨立.
(Ⅰ)設“恰好二人破譯出密碼”為事件B,則有B=A1?A2?![]() ?A1?
?A1?![]() ?A3+
?A3+![]() ?A2?A3且A1?A2?
?A2?A3且A1?A2?![]() ,A1?
,A1?![]() ?A3,
?A3,![]() ?A2?A3彼此互斥
?A2?A3彼此互斥
于是P(B)=P(A1?A2?![]() )+P(A1?
)+P(A1?![]() ?A3)+P(
?A3)+P(![]() ?A2?A3)
?A2?A3)
=![]()
=![]() .
.
答:恰好二人破譯出密碼的概率為![]() .
.
(Ⅱ)設“密碼被破譯”為事件C,“密碼未被破譯”為事件D.
D=![]() ?
?![]() ?
?![]() ,且
,且![]() ,
,![]() ,
,![]() 互相獨立,則有
互相獨立,則有
P(D)=P(![]() )?P(
)?P(![]() )?P(
)?P(![]() )=
)=![]() =
=![]() .
.
而P(C)=1-P(D)=![]() ,故P(C)>P(D).
,故P(C)>P(D).
答:密碼被破譯的概率比密碼未被破譯的概率大.


科目:高中數學 來源: 題型:
| 1 |
| 5 |
| 1 |
| 4 |
| 1 |
| 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 6 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
查看答案和解析>>
科目:高中數學 來源:2010-2011學年北京市西城區高三一模試卷數學(理科) 題型:解答題
甲、乙、丙三人獨立破譯同一份密碼,已知甲、乙、丙各自破譯出密碼的概率分別為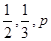 .且他們是否破譯出密碼互不影響.若三人中只有甲破譯出密碼的概率為
.且他們是否破譯出密碼互不影響.若三人中只有甲破譯出密碼的概率為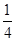 .
.
(Ⅰ)求甲乙二人中至少有一人破譯出密碼的概率;
(Ⅱ)求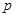 的值;
的值;
(Ⅲ)設甲、乙、丙三人中破譯出密碼的人數為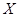 ,求
,求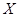 的分布列和數學期望
的分布列和數學期望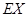 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com