
【題目】如果一個數列從第2項起,每一項與它前一項的差都大于2,則稱這個數列為“阿當數列”.
(1)若數列![]() 為“阿當數列”,且
為“阿當數列”,且![]() ,
,![]() ,
,![]() ,求實數
,求實數![]() 的取值范圍;
的取值范圍;
(2)是否存在首項為1的等差數列![]() 為“阿當數列”,且其前
為“阿當數列”,且其前![]() 項和
項和![]() 滿足
滿足![]() ?若存在,請求出
?若存在,請求出![]() 的通項公式;若不存在,請說明理由.
的通項公式;若不存在,請說明理由.
(3)已知等比數列![]() 的每一項均為正整數,且
的每一項均為正整數,且![]() 為“阿當數列”,
為“阿當數列”,![]() ,
,![]() ,當數列
,當數列![]() 不是“阿當數列”時,試判斷數列
不是“阿當數列”時,試判斷數列![]() 是否為“阿當數列”,并說明理由.
是否為“阿當數列”,并說明理由.
【答案】(1)![]() ;(2)不存在,理由見詳解;(3)見詳解.
;(2)不存在,理由見詳解;(3)見詳解.
【解析】
(1)根據題意,得到![]() ,求解即可得出結果;
,求解即可得出結果;
(2)先假設存在等差數列![]() 為“阿當數列”,設公差為
為“阿當數列”,設公差為![]() ,則
,則![]() ,根據等差數列求和公式,結合題中條件,得到
,根據等差數列求和公式,結合題中條件,得到![]() ,即
,即![]() 對任意
對任意![]() 都成立,判斷出
都成立,判斷出![]() ,推出矛盾,即可得出結果;
,推出矛盾,即可得出結果;
(3)設等比數列![]() 的公比為
的公比為![]() ,根據
,根據![]() 為“阿當數列”,推出在數列
為“阿當數列”,推出在數列![]()
![]() 中,
中,![]() 為最小項;在數列
為最小項;在數列![]()
![]() 中,
中,![]() 為最小項;得到
為最小項;得到![]() ,
,![]() ,再由數列
,再由數列![]() 每一項均為正整數,得到
每一項均為正整數,得到![]() ,
,![]() 或
或![]() ,
,![]() ;分別討論
;分別討論![]() ,
,![]() 和
和![]() ,
,![]() 兩種情況,結合數列的增減性,即可得出結果.
兩種情況,結合數列的增減性,即可得出結果.
(1)由題意可得:![]() ,
,![]() ,
,
即![]() ,解得
,解得![]() 或
或![]() ;
;
所以實數![]() 的取值范圍是
的取值范圍是![]() ;
;
(2)假設存在等差數列![]() 為“阿當數列”,設公差為
為“阿當數列”,設公差為![]() ,則
,則![]() ,
,
由![]() 可得:
可得:![]() ,
,
又![]() ,所以
,所以![]() 對任意
對任意![]() 都成立,
都成立,
即![]() 對任意
對任意![]() 都成立,
都成立,
因為![]() ,且
,且![]() ,所以
,所以![]() ,與
,與![]() 矛盾,
矛盾,
因此,不存在等差數列![]() 為“阿當數列”;
為“阿當數列”;
(3)設等比數列![]() 的公比為
的公比為![]() ,則
,則![]() ,且每一項均為正整數,
,且每一項均為正整數,
因為![]() 為“阿當數列”,所以
為“阿當數列”,所以![]() ,
,
所以![]() ,
,![]() ;因為
;因為![]() ,
,
即在數列![]()
![]() 中,
中,![]() 為最小項;
為最小項;
同理,在數列![]()
![]() 中,
中,![]() 為最小項;
為最小項;
由![]() 為“阿當數列”,只需
為“阿當數列”,只需![]() ,即
,即![]() ,
,
又因為數列![]() 不是“阿當數列”,所以
不是“阿當數列”,所以![]() ,即
,即![]() ,
,
由數列![]() 每一項均為正整數,可得:
每一項均為正整數,可得:![]() ,所以
,所以![]() ,
,![]() 或
或![]() ,
,![]() ;
;
當![]() ,
,![]() 時,
時,![]() ,則
,則![]() ,
,
令![]() ,則
,則![]() ,
,
所以![]() ,
,
即數列![]() 為遞增數列,
為遞增數列,
所以![]() ,
,
因為![]() ,所以對任意
,所以對任意![]() ,都有
,都有![]() ,
,
即數列![]() 是“阿當數列”;
是“阿當數列”;
當![]() ,
,![]() 時,
時,![]() ,則
,則![]() ,
,
顯然數列![]() 是遞減數列,
是遞減數列,![]() ,
,
故數列![]() 不是“阿當數列”;
不是“阿當數列”;
綜上,當![]() 時,數列
時,數列![]() 是“阿當數列”;當
是“阿當數列”;當![]() 時,數列
時,數列![]() 不是“阿當數列”.
不是“阿當數列”.


科目:高中數學 來源: 題型:
【題目】如圖,在直三棱柱![]() 中,
中,![]() ,
,![]() ,點
,點![]() 為棱
為棱![]() 的中點,點
的中點,點![]() 為線段
為線段![]() 上一動點.
上一動點.

(Ⅰ)求證:當點![]() 為線段
為線段![]() 的中點時,
的中點時,![]() 平面
平面![]() ;
;
(Ⅱ)設![]() ,試問:是否存在實數
,試問:是否存在實數![]() ,使得平面
,使得平面![]() 與平面
與平面![]() 所成銳二面角的余弦值為
所成銳二面角的余弦值為![]() ?若存在,求出這個實數
?若存在,求出這個實數![]() ;若不存在,請說明理由.
;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】國家放開計劃生育政策,鼓勵一對夫婦生育2個孩子.在某地區的100000對已經生育了一胎夫婦中,進行大數據統計得,有100對第一胎生育的是雙胞胎或多胞胎,其余的均為單胞胎.在這99900對恰好生育一孩的夫婦中,男方、女方都愿意生育二孩的有50000對,男方愿意生育二孩女方不愿意生育二孩的有![]() 對,男方不愿意生育二孩女方愿意生育二孩的有
對,男方不愿意生育二孩女方愿意生育二孩的有![]() 對,其余情形有
對,其余情形有![]() 對,且
對,且![]() .現用樣本的頻率來估計總體的概率.
.現用樣本的頻率來估計總體的概率.
(1)說明“其余情形”指何種具體情形,并求出![]() ,
,![]() ,
,![]() 的值;
的值;
(2)該地區為進一步鼓勵生育二孩,實行貼補政策:凡第一胎生育了一孩的夫婦一次性貼補5000元,第一胎生育了雙胞胎或多胞胎的夫婦只有一次性貼補15000元.第一胎已經生育了一孩再生育了二孩的夫婦一次性再貼補20000元.這種補貼政策直接提高了夫婦生育二孩的積極性:原先男方或女方中只有一方愿意生育二孩的夫婦現在都愿意生育二孩,但原先男方、女方都不愿意生育二孩的夫婦仍然不愿意生育二孩.設![]() 為該地區的一對夫婦享受的生育貼補,求
為該地區的一對夫婦享受的生育貼補,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】國慶期間,一位游客來到某旅游城市,這里有甲、乙、丙三個著名的旅游景點,若這位游客游覽這三個景點的概率分別是![]() ,且客人是否游覽哪個景點互不影響,設
,且客人是否游覽哪個景點互不影響,設![]() 表示客人離開該城市時游覽的景點數與沒有游覽的景點數之差的絕對值.
表示客人離開該城市時游覽的景點數與沒有游覽的景點數之差的絕對值.
(Ⅰ)求![]() 的分布列和數學期望;
的分布列和數學期望;
(Ⅱ)記“![]() 時,不等式
時,不等式![]() 恒成立”為事件
恒成立”為事件![]() ,求事件
,求事件![]() 發生的概率.
發生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學為提升學生的英語學習能力,進行了主題分別為“聽”、“說”、“讀”、“寫”四場競賽.規定:每場競賽的前三名得分分別為![]() ,
, ![]() ,
, ![]() (
(![]() ,且
,且![]() ,
, ![]() ,
, ![]() ),選手的最終得分為各場得分之和.最終甲、乙、丙三人包攬了每場競賽的前三名,在四場競賽中,已知甲最終分為
),選手的最終得分為各場得分之和.最終甲、乙、丙三人包攬了每場競賽的前三名,在四場競賽中,已知甲最終分為![]() 分,乙最終得分為
分,乙最終得分為![]() 分,丙最終得分為
分,丙最終得分為![]() 分,且乙在“聽”這場競賽中獲得了第一名,則“聽”這場競賽的第三名是( )
分,且乙在“聽”這場競賽中獲得了第一名,則“聽”這場競賽的第三名是( )
A. 甲 B. 乙 C. 丙 D. 甲和丙都有可能
查看答案和解析>>
科目:高中數學 來源: 題型:
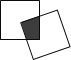
【題目】現有一個關于平面圖形的命題:如圖,同一平面內有兩個邊長都是2的正方形,其中一個的某頂點在另一個的中心,則這兩個正方形重疊部分的面積恒為______.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com