
【題目】已知數列{an},{bn}滿足2Sn=(an+2)bn , 其中Sn是數列{an}的前n項和.
(1)若數列{an}是首項為 ![]() ,公比為﹣
,公比為﹣ ![]() 的等比數列,求數列{bn}的通項公式;
的等比數列,求數列{bn}的通項公式;
(2)若bn=n,a2=3,求證:數列{an}滿足an+an+2=2an+1 , 并寫出數列{an}的通項公式;
(3)在(2)的條件下,設cn= ![]() , 求證:數列{cn}中的任意一項總可以表示成該數列其他兩項之積.
, 求證:數列{cn}中的任意一項總可以表示成該數列其他兩項之積.
【答案】
(1)解:因為數列{an}是首項為 ![]() ,公比為-
,公比為- ![]() 的等比數列
的等比數列
所以 ![]() ,
, ![]()
所以 ![]()
(2)解:若bn=n,則2Sn=(an+2)n,所以2Sn+1=(n+1)(an+1+2)
所以2an+1=(n+1)an+1﹣nan+2,即(n﹣1)an+1+2=nan
所以nan+2+2=(n+1)an+1
所以nan+2﹣(n﹣1)an+1=(n+1)an+1﹣nan
所以an+an+2=2an+1
又由2S1=a1+2,得:a1=2
所以數列{an}是首項為2公差為1的等差數列
所以an=n+1
(3)解:證明:由(2)知 ![]() ,
,
對于給定的n∈N*,若存在k,t≠n,且t,k∈N*,使得cn=ckct,
只需 ![]()
只需 ![]()
取k=n+1,則t=n(n+2)
所以對于數列{cn}中的任意一項 ![]() ,
,
都存在Cn+1= ![]() 與Cn(n+2)=
與Cn(n+2)= ![]() ,使得cn=cn+1cn(n+2),
,使得cn=cn+1cn(n+2),
即數列{cn}中的任意一項總可以表示成該數列其他兩項之積
【解析】(1)通過數列{an}是首項為 ![]() ,公比為-
,公比為- ![]() 的等比數列求出通項公式,然后求解
的等比數列求出通項公式,然后求解 ![]() .(2)若bn=n,通過an=Sn﹣Sn+1 , 得到遞推關系式,化簡推出數列{an}是首項為2公差為1的等差數列,求出通項公式.(3)由(2)知
.(2)若bn=n,通過an=Sn﹣Sn+1 , 得到遞推關系式,化簡推出數列{an}是首項為2公差為1的等差數列,求出通項公式.(3)由(2)知 ![]() ,對于給定的n∈N* , 若存在k,t≠n,且t,k∈N* , 使得cn=ckct , 證明
,對于給定的n∈N* , 若存在k,t≠n,且t,k∈N* , 使得cn=ckct , 證明 ![]() ,構造
,構造 ![]() ,然后證明數列{cn}中的任意一項總可以表示成該數列其他兩項之積.
,然后證明數列{cn}中的任意一項總可以表示成該數列其他兩項之積.
【考點精析】認真審題,首先需要了解數列的前n項和(數列{an}的前n項和sn與通項an的關系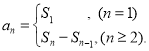 ),還要掌握數列的通項公式(如果數列an的第n項與n之間的關系可以用一個公式表示,那么這個公式就叫這個數列的通項公式)的相關知識才是答題的關鍵.
),還要掌握數列的通項公式(如果數列an的第n項與n之間的關系可以用一個公式表示,那么這個公式就叫這個數列的通項公式)的相關知識才是答題的關鍵.


 開心快樂假期作業暑假作業西安出版社系列答案
開心快樂假期作業暑假作業西安出版社系列答案 名題訓練系列答案
名題訓練系列答案科目:高中數學 來源: 題型:
【題目】如圖,三棱柱ABC﹣A1B1C1中,側面AA1C1C⊥底面ABC,AA1=A1C=AC=2,AB=BC且AB⊥BC, 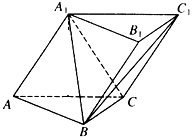
(Ⅰ)求證:AC⊥A1B;
(Ⅱ)求二面角A﹣A1C﹣B的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2﹣2ax(a>0).
(1)當a=2時,解關于x的不等式﹣3<f(x)<5;
(2)對于給定的正數a,有一個最大的正數M(a),使得在整個區間[0,M(a)]上,不等式|f(x)|≤5恒成立.求出M(a)的解析式;
(3)函數y=f(x)在[t,t+2]的最大值為0,最小值是﹣4,求實數a和t的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,橫、縱坐標均為整數的點叫做格點.若函數y=f(x)的圖象恰好經過k個格點,則稱函數y=f(x)為k階格點函數.已知函數:①y=x2;②y=2sinx,③y=πx﹣1;④y=cos(x+ ![]() ).其中為一階格點函數的序號為(注:把你認為正確論斷的序號都填上)
).其中為一階格點函數的序號為(注:把你認為正確論斷的序號都填上)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】用數學歸納法證明1+2+3+…+n2= ![]() ,則當n=k+1時左端應在n=k的基礎上加上( )
,則當n=k+1時左端應在n=k的基礎上加上( )
A.k2+1
B.(k+1)2
C.![]()
D.(k2+1)+(k2+2)+(k2+3)+…+(k+1)2
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=lnx﹣x.
(1)求函數f(x)的單調區間;
(2)若方程f(x)=m(m<﹣2)有兩個相異實根x1 , x2 , 且x1<x2 , 證明:x1x22<2.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}的前n項和 ![]() ,數列{bn}的前n項和為Bn .
,數列{bn}的前n項和為Bn .
(1)求數列{an}的通項公式;
(2)設 ![]() ,求數列{cn}的前n項和Cn;
,求數列{cn}的前n項和Cn;
(3)證明: ![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com