解:(Ⅰ)
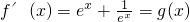
,
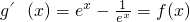
,
∴直線l
1的斜率
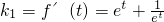
,直線l
2的斜率

,
令k
1=k
2,得
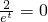
,此方程沒有實數解,∴不論t取何實數值,直線l
1與l
2恒相交.
(Ⅱ)直線l
1的方程為:y=f(t)+g(t)(x-t),…①
直線l
2的方程為:y=g(t)+f(t)(x-t),…②
由①、②得:(g(t)-f(t))(x-t-1)=0.
∵

,∴x-t=1,又∵直線AB方程為x=t,直線AB垂直x軸,∴點P到直線AB的距離為1.
(Ⅲ)由(Ⅱ)可求得P(t+1,2e
t),
①∵
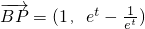
,
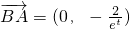
,
∴
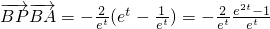
,
∵t<0,e
2t<1,∴

,
又∵
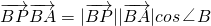
,
∴cos∠B>0,∠B恒為銳角.
②∵
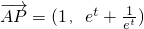
,
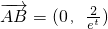
,
∴
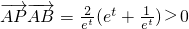
,
∴不論t取何值,∠A恒為銳角.
③∵
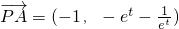
,
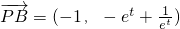
,∴
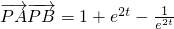
.
令
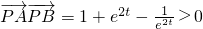
,得(e
2t)
2+e
2t-1>0,
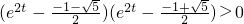
,
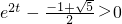
,
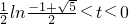
.
又∵
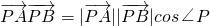
,∴cos∠P>0,∠P為銳角.
令
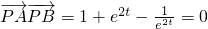
,得
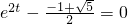
,
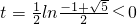
,
此時,cos∠P=0,∠P為直角;
令
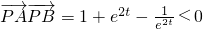
,得(e
2t)
2+e
2t-1<0,
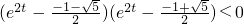
,
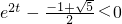
,
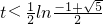
,此時,cos∠P<0,∠P為鈍角.
綜合①②③得:當
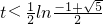
時,△PAB為鈍角三角形;
當
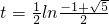
時,△PAB為直角三角形;
當
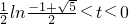
時,△PAB為銳角三角形.
分析:(Ⅰ)求出兩個函數的導數,即得切線的斜率,令這兩條切線的斜率相等,此方程無解,故這兩條切線的斜率一定不相等,得到直線l
1與l
2恒相交.
(Ⅱ)用點斜式求得直線l
1和直線l
2的方程,求得交點P的橫坐標滿足x-t=1,又直線AB方程為x=t,直線AB垂直x軸,
故點P到直線AB的距離為 1.
(Ⅲ)利用兩個向量的數量積的定義、數量積公式可得∠B恒為銳角,且∠A恒為銳角,令

分別小于0、等于
0、小于0,求出對應的t值,即得所求.
點評:本題考查導數的幾何意義,點到直線的距離公式,兩個向量的數量積的定義,數量積公式,三角形形狀的判定,體現了分類討論的數學思想.

 ,
, ,動直線x=t分別與函數y=f(x)、y=g(x)的圖象分別交于點A(t,f(t))、B(t,g(t)),在點A處作函數y=f(x)的圖象的切線,記為直線l1,在點B處作函數y=g(x)的圖象的切線,記為直線l2.
,動直線x=t分別與函數y=f(x)、y=g(x)的圖象分別交于點A(t,f(t))、B(t,g(t)),在點A處作函數y=f(x)的圖象的切線,記為直線l1,在點B處作函數y=g(x)的圖象的切線,記為直線l2.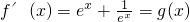 ,
,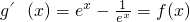 ,
,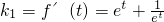 ,直線l2的斜率
,直線l2的斜率 ,
,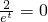 ,此方程沒有實數解,∴不論t取何實數值,直線l1與l2恒相交.
,此方程沒有實數解,∴不論t取何實數值,直線l1與l2恒相交. ,∴x-t=1,又∵直線AB方程為x=t,直線AB垂直x軸,∴點P到直線AB的距離為1.
,∴x-t=1,又∵直線AB方程為x=t,直線AB垂直x軸,∴點P到直線AB的距離為1.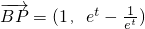 ,
,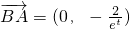 ,
,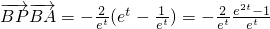 ,
, ,
,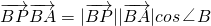 ,
,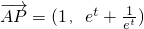 ,
,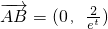 ,
,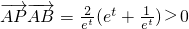 ,
,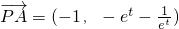 ,
,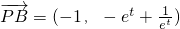 ,∴
,∴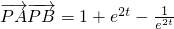 .
.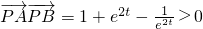 ,得(e2t)2+e2t-1>0,
,得(e2t)2+e2t-1>0,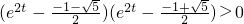 ,
,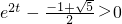 ,
,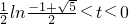 .
.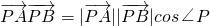 ,∴cos∠P>0,∠P為銳角.
,∴cos∠P>0,∠P為銳角.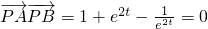 ,得
,得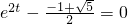 ,
,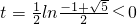 ,
,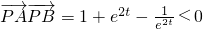 ,得(e2t)2+e2t-1<0,
,得(e2t)2+e2t-1<0,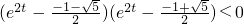 ,
,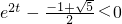 ,
,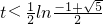 ,此時,cos∠P<0,∠P為鈍角.
,此時,cos∠P<0,∠P為鈍角.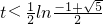 時,△PAB為鈍角三角形;
時,△PAB為鈍角三角形;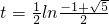 時,△PAB為直角三角形;
時,△PAB為直角三角形;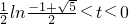 時,△PAB為銳角三角形.
時,△PAB為銳角三角形. 分別小于0、等于
分別小于0、等于
