【題目】已知數列
是公差為
的等差數列，如果數列
滿足
，則稱數列
是“可等距劃分數列”．
（1）判斷數列
是否是“可等距劃分數列”，并說明理由；
（2）已知
，
，設
，求證：對任意的
，
，數列
都是“可等距劃分數列”；
（3）若數列
是“可等距劃分數列”，求
的所有可能值．
【答案】（1）數列
是“可等距劃分數列”，理由見解析；（2）證明見解析；（3）
【解析】
（1）存在等差數列
使得不等式成立，進而可知是“可等距劃分數列”；
（2）設等差數列
，且
，可知
，得到符合題意的不等式，證得結論；
（3）當
時，可得到等差數列
滿足條件；當
時，可得到
滿足條件；當
時，采用反證法，若有等差數列
滿足條件，由
可求得
，不滿足條件，從而知不合題意，從而得到結果.
（1）存在等差數列，使得
數列是“可等距劃分數列”
（2）對任意的
，
，設
則對任意的
，都有
即數列為等差數列
，
即滿足
對任意的，，數列
都是“可等距劃分數列”
（3）當時，對于數列
存在等差數列滿足條件
當時，對于數列
存在等差數列滿足條件
當時，若存在等差數列滿足
則有
，
，與
矛盾
當時，若數列
不可能是“可等距劃分數列”
綜上所述，
的所有可能值是
，
備戰中考寒假系列答案科目：高中數學 來源： 題型：
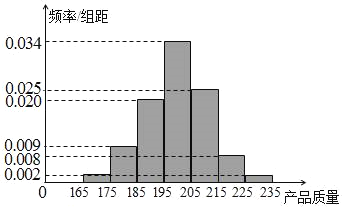
【題目】某企業為了檢查甲、乙兩條自動包裝流水線的生產情況，隨機在這兩條流水線上各抽取
件產品作為樣本稱出它們的質量（單位：毫克），質量值落在
的產品為合格品，否則為不合格品．如表是甲流水線樣本頻數分布表，如圖是乙流水線樣本的頻率分布直方圖．
產品質量/毫克 | 頻數 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
（Ⅰ）以樣本的頻率作為概率，試估計從甲流水線上任取
件產品，求其中不合格品的件數
的數學期望．
甲流水線 | 乙流水線 | 總計 | |
合格品 | |||
不合格品 | |||
總計 |
（Ⅱ）由以上統計數據完成下面
列聯表，能否在犯錯誤的概率不超過
的前提下認為產品的包裝合格與兩條自動包裝流水線的選擇有關？
（Ⅲ）由乙流水線的頻率分布直方圖可以認為乙流水線生產的產品質量
服從正態分布
，求質量落在
上的概率．
參考公式：
參考數據：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
參考公式：
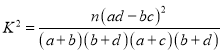，其中
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某校在一次期末數學測試中，為統計學生的考試情況，從學校的2000名學生中隨機抽取50名學生的考試成績，被測學生成績全部介于65分到145分之間（滿分150分），將統計結果按如下方式分成八組：第一組
，
，第二組
，
，
第八組
，
，如圖是按上述分組方法得到的頻率分布直方圖的一部分．
（1）求第七組的頻率，并完成頻率分布直方圖；
（2）用樣本數據估計該校的2000名學生這次考試成績的平均分（同一組中的數據用該組區間的中點值代表該組數據平均值）；
（3）若從樣本成績屬于第六組和第八組的所有學生中隨機抽取2名，求他們的分差的絕對值小于10分的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知點
為圓
的圓心， 
是圓上的動點，點
在圓的半徑
上，且有點
和
上的點
，滿足
， 
.
（1）當點
在圓上運動時，求點
的軌跡方程；
（2）若斜率為
的直線
與圓
相切，直線
與（1）中所求點
的軌跡交于不同的兩點
， 
， 
是坐標原點，且
時，求
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
