
如圖,曲線y=![]() 上的點Pi(
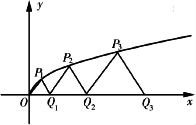
上的點Pi(![]() ,ti)(i=1,2,…,n,…)與x軸正半軸上的點Qi及原點O構成一系列正三角形PiQi-1Qi(Q0與O重合),記an=|QnQn-1|.
,ti)(i=1,2,…,n,…)與x軸正半軸上的點Qi及原點O構成一系列正三角形PiQi-1Qi(Q0與O重合),記an=|QnQn-1|.
(Ⅰ)求a1的值;
(Ⅱ)求數列{an}的通項公式an;
(Ⅲ)設Sn為數列{an}的前n項和;若對于任意的實數λ∈[0,1],總存在自然數k,當n≥k時,3Sn-3n+2≥(1-λ)(3an-1)恒成立,求k的最小值.
 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源:南通高考密卷·數學(理) 題型:044
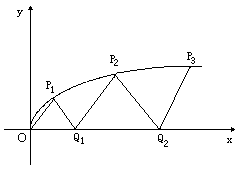
如圖,曲線y2=x(y≥0)上的點Pi與x軸的正半軸上的點Qi及原點O構成一系列正三角形:△OP1Q1,△Q1P2Q2,…,△Qn-1PnQn,….設正三角形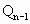 PnQn的邊長為an,n∈N*(記Q0為O),Qn(Sn,0).
PnQn的邊長為an,n∈N*(記Q0為O),Qn(Sn,0).
(1)求a1的值;
(2)求數列{an}的通項公式an;
(3)求證:當n≥2時,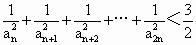 .
.
查看答案和解析>>
科目:高中數學 來源:湖南常德市2007-2008學年度高三數學水平檢測考試題(理科) 題型:044
如圖:曲線y=x2(x≥0)上的點Pi與y軸正半軸上的點Qi及原點O構成一系列以Pi為直角頂點的等腰直角三角形△OP1Q1,△Q1P2Q2,…,△Qn-1PnQn(Q0為坐標原點O).設△Qn-1PnQn的斜邊長為an,n∈N*.
(Ⅰ)求a1,a2的值;
(Ⅱ)求數列{an}的通項公式;
(Ⅲ)求證:![]()
查看答案和解析>>
科目:高中數學 來源:河南省平頂山新鄉許昌市2009-2010學年高三第三次調研考試理科數學試題 題型:044
如圖,點An(xn,yn)是曲線y2=2x(y≥0)上的點,點Bn(an,0)是x軸上的點,△Bn-1AnBn是以An為直角頂點的等腰直角三角形,其中n=1,2,3,…,B0為坐標原點.
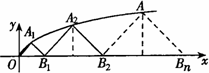
(Ⅰ)求數列{an}的通項公式;
(Ⅱ)設數列bn=2n-1,求最小正整數m,使得對任意的n∈N*,當n>m時,an<bn成立.
查看答案和解析>>
科目:高中數學 來源:安徽省合肥市2012屆高三第二次教學質量檢測數學文科試題 題型:044
如圖所示,設曲線y=![]() 上的點與x軸上的點順次構成等腰直角三角形△OB1A1,△A1B2A2,…,,直角頂點在曲線y=
上的點與x軸上的點順次構成等腰直角三角形△OB1A1,△A1B2A2,…,,直角頂點在曲線y=![]() 上,設A1的坐標為(an,0),A0為原點
上,設A1的坐標為(an,0),A0為原點

(1)求a1,并求出an和an-1(n∈N*)之間的關系式;
(2)求數列{an}的通項公式;
(3)設bn=![]() (n∈N*),求數列{bn}的前n項和Sn
(n∈N*),求數列{bn}的前n項和Sn
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com