【答案】
分析:(1)確定數列{b
n}的前3項,利用等差數列的定義,即可確定實數t的值;
(2)先確定c
m+1必是數列{a
n}中的某一項a
k+1,再分組求和,結合整除的性質,即可得到結論.
解答:解:(1)當n=1時,
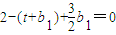
,得b
1=2t-4,
同理:n=2時,得b
2=16-4t;n=3時,得b
3=12-2t,則由b
1+b
3=2b
2,得t=3.…(2分)
而當t=3時,
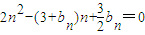
,得b
n=2n
由b
n+1-b
n=2,知此時數列{b
n}為等差數列.…(4分)
(2)由題意知,c
1=a
1=2,c
2=c
3=2,c
4=a
2=4,c
5=c
6=c
7=c
8=2,c
9=a
3=8,…
則當m=1時,T
1=2≠2c
2=4,不合題意,舍去;
當m=2時,T
2=c
1+c
2=4=2c
3,所以m=2成立; …(6分)
當m≥3時,若c
m+1=2,則T
m≠2c
m+1,不合題意,舍去;
從而c
m+1必是數列{a
n}中的某一項a
k+1,則
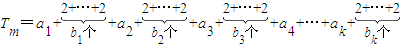
=(2+2
2+2
3+…+2
k)+2(b
1+b
2+b
3+…+b
k)=
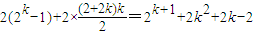
,…(9分)
又

,
所以2
k+1+2k
2+2k-2=2×2
k+1,即2
k-k
2-k+1=0,
所以2
k+1=k
2+k=k(k+1)
因為2
k+1(k∈N
*)為奇數,而k
2+k=k(k+1)為偶數,所以上式無解.
即當m≥3時,T
m≠2c
m+1綜上所述,滿足題意的正整數僅有m=2.…(12分)
點評:本題考查等差數列的判定,考查數列的求和,考查學生分析解決問題的能力,考查學生的計算能力,屬于中檔題.

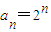 ,數列{bn}滿足
,數列{bn}滿足 ,(t∈R,n∈N*).
,(t∈R,n∈N*).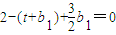 ,得b1=2t-4,
,得b1=2t-4,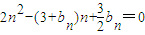 ,得bn=2n
,得bn=2n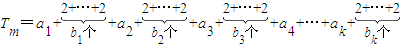
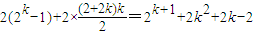 ,…(9分)
,…(9分) ,
,
