
【題目】已知函數![]() ,
,![]() 為自然對數的底數.
為自然對數的底數.
(1)求證:當![]() 時,
時,![]() ;
;
(2)若函數![]() 有兩個零點,求實數
有兩個零點,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)見解析;(2)![]() .
.
【解析】
(1)構造![]() ,再求導可得
,再求導可得![]() ,再對導數求導,繼而分析導函數的正負區間進而求得原函數的單調區間求最小值證明即可.
,再對導數求導,繼而分析導函數的正負區間進而求得原函數的單調區間求最小值證明即可.
(2) 求導可得![]() ,再分
,再分![]() ,
,![]() ,
,![]() 分析函數的最小值,同時根據零點存在性定理判斷是否有兩個零點即可.
分析函數的最小值,同時根據零點存在性定理判斷是否有兩個零點即可.
(1)設![]() …
…
∴![]() ,
,
∴![]()
∵![]() ∴
∴![]() ∴
∴![]()
∴![]() 在
在![]() 上單調遞增,
上單調遞增,
又![]()
∴![]() 時,
時,![]()
∴![]() 在
在![]() 上單調遞增,
上單調遞增,
又![]()
∴![]() 時,
時,![]()
故當![]() 時,
時,![]() ;
;
(2)∵![]()
∴![]() ,
,
①當![]() 時,易知函數
時,易知函數![]() 只有一個零點,不符合題意;
只有一個零點,不符合題意;
②當![]() 時,在
時,在![]() 上,
上,![]() ,
,![]() 單調遞減;在
單調遞減;在![]() 上,
上,![]() ,
,![]() 單調遞增;又
單調遞增;又![]() ,且
,且![]() ,且當
,且當![]() 上,
上,![]() 恒成立,
恒成立,
又不妨取![]() 且
且![]() 時,
時,![]()
或者考慮:當![]()
所以函數![]() 在
在![]() 和在
和在![]() 上各有一個零點,即有兩個零點.
上各有一個零點,即有兩個零點.
③當![]() 時,由
時,由![]() 得
得![]() 或
或![]()
(i)當![]() 即
即![]() 時,在
時,在![]() 上,
上,![]() 成立,故
成立,故![]() 在
在![]() 上單調遞增,所以函數
上單調遞增,所以函數![]() 至多有一個零點,不符合題意
至多有一個零點,不符合題意
(ii)當![]() 即
即![]() 時,在
時,在![]() 和
和![]() 上,
上,![]() ,
,![]() 單調遞增;
單調遞增;
在![]() 上
上![]() ,
,![]() 單調遞減;
單調遞減;
又![]() ,且
,且![]() ,
,
所以函數![]() 至多有一個零點,不符合題意
至多有一個零點,不符合題意
(iii)當![]() 即
即![]() 時,在
時,在![]() 和
和![]() 上
上![]() ,
,![]() 單調遞增;在
單調遞增;在![]() 上
上![]() ,
,![]() 單調遞減;又
單調遞減;又![]() ,所以函數
,所以函數![]() 至多有一個零點,不符合題意
至多有一個零點,不符合題意
綜上所述:實數![]() 的取值范圍是
的取值范圍是![]()


科目:高中數學 來源: 題型:
【題目】已知數列![]() 滿足:
滿足:![]() (常數
(常數![]() ),
),![]() ,(
,(![]() ,
,![]() ).數列
).數列![]() 滿足:
滿足:![]()
![]() .
.
(1)分別求![]() ,
,![]() ,
,![]() 的值:
的值:
(2)求數列![]() 的通項公式;
的通項公式;
(3)問:數列![]() 的每一項能否均為整數?若能,求出
的每一項能否均為整數?若能,求出![]() 的所有可能值;若不能,請說明理由.
的所有可能值;若不能,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】改革開放以來,我國農村7億多貧困人口擺脫貧困,貧困發生率由1978年的97.5%下降到2018年底的1.4%,創造了人類減貧史上的中國奇跡,為全球減貧事業貢獻了中國智慧和中國方案.“貧困發生率”是指低于貧困線的人口占全體人口的比例.2012年至2018年我國貧困發生率的數據如下表:
年份( | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
貧困發生率 | 10.2 | 8.5 | 7.2 | 5.7 | 4.5 | 3.1 | 1.4 |
(1)從表中所給的7個貧困發生率數據中任選兩個,求至少有一個低于5%的概率;
(2)設年份代碼![]() ,利用回歸方程,分析2012年至2018年貧困發生率的變化情況,并預測2019年貧困發生率.
,利用回歸方程,分析2012年至2018年貧困發生率的變化情況,并預測2019年貧困發生率.
附:回歸直線![]() 的斜率和截距的最小二乘估計公式分別為:
的斜率和截距的最小二乘估計公式分別為: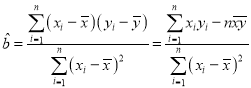 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在多面體![]() 中,四邊形
中,四邊形![]() 為矩形,
為矩形,![]() ,
,![]() 均為等邊三角形,
均為等邊三角形,![]() ,
,![]() .
.
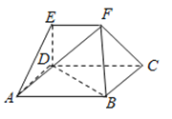
(Ⅰ)過![]() 作截面與線段
作截面與線段![]() 交于點
交于點![]() ,使得
,使得![]() 平面
平面![]() ,試確定點
,試確定點![]() 的位置,并予以證明;
的位置,并予以證明;
(Ⅱ)在(Ⅰ)的條件下,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的右焦點F到左頂點的距離為3.
的右焦點F到左頂點的距離為3.
(1)求橢圓C的方程;
(2)設O是坐標原點,過點F的直線與橢圓C交于A,B兩點(A,B不在x軸上),若![]() ,延長AO交橢圓與點G,求四邊形AGBE的面積S的最大值.
,延長AO交橢圓與點G,求四邊形AGBE的面積S的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某種產品的質量以其質量指標值衡量,質量指標值越大表明質量越好,記其質量指標值為M,當M≥85時,產品為一級品;當75≤M<85時,產品為二級品;當70≤M<75時,產品為三級品.現用兩種新配方(分別稱為A配方和B配方)做實驗,各生產了100件這種產品,并測量了每件產品的質量指標值,得到下面試驗結果:
A配方的頻數分布表

B配方的頻數分布表

(1)從A配方生產的產品中按等級分層抽樣抽取5件產品,再從這5件產品中任取3件,求恰好取到1件二級品的頻率;
(2)若這種新產品的利潤率y與質量指標M滿足如下條件: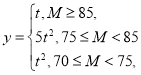 其中t∈
其中t∈![]() ,請分別計算兩種配方生產的產品的平均利潤率,如果從長期來看,你認為投資哪種配方的產品平均利潤率較大?
,請分別計算兩種配方生產的產品的平均利潤率,如果從長期來看,你認為投資哪種配方的產品平均利潤率較大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,角A,B,C的對邊分別為a,b,c,滿足acosB+bcosA=2ccosC.
(1)求角C的大小;
(2)若△ABC的周長為3,求△ABC的內切圓面積S的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在等腰梯形ABCD中,AB//CD,∠ABC=![]() ,BC=CD=CE=1,EC⊥平面ABCD,EF
,BC=CD=CE=1,EC⊥平面ABCD,EF![]() AC,P是線段EF上的動點
AC,P是線段EF上的動點
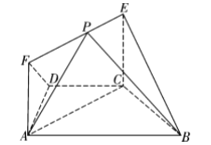
(1)求證:平面BCE⊥平面ACEF;
(2)求平面PAB與平面BCE所成銳二面角![]() 的最小值
的最小值
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com