
【題目】已知橢圓![]() 與y軸的正半軸相交于點M,且橢圓E上相異兩點A、B滿足直線MA,MB的斜率之積為
與y軸的正半軸相交于點M,且橢圓E上相異兩點A、B滿足直線MA,MB的斜率之積為![]() .
.
(Ⅰ)證明直線AB恒過定點,并求定點的坐標;
(Ⅱ)求三角形ABM的面積的最大值.
【答案】(1)直線![]() 恒過定點
恒過定點![]() .(2)
.(2)![]()
【解析】試題分析:利用設而不求思想設出點的坐標,首先考慮 直線斜率不存在的情況,然后研究直線斜率存在的一般情況,設出直線斜截式方程與橢圓方程聯立方程組,代入整理后寫出根與系數關系,根據MA、MB的斜率之積為![]() ,代入
,代入![]() ,解出
,解出![]() ,得出直線過定點
,得出直線過定點![]() ,第二步聯立方程組后利用判別式大于零,求出k的范圍,表示三角形的面積,利用基本不等式求出最值 .
,第二步聯立方程組后利用判別式大于零,求出k的范圍,表示三角形的面積,利用基本不等式求出最值 .
試題解析:
解:(Ⅰ)由橢圓![]() 的方程得,上頂點
的方程得,上頂點![]() ,記
,記![]() 由題意知,
由題意知, ![]() ,若直線
,若直線![]() 的斜率不存在,則直線
的斜率不存在,則直線![]() 的方程為
的方程為![]() ,故
,故![]() ,且
,且 ,因此
,因此![]() ,與已知不符,因此直線
,與已知不符,因此直線![]() 的斜率存在,設直線
的斜率存在,設直線![]() :
: ![]() ,代入橢圓
,代入橢圓![]() 的方程
的方程![]() 得:
得: ![]()
![]() ………①
………①
因為直線![]() 與曲線
與曲線![]() 有公共點
有公共點![]() ,所以方程①有兩個非零不等實根
,所以方程①有兩個非零不等實根![]() ,
,
所以![]() ,
,
又![]() ,
, ![]() ,
,
由![]() ,得
,得![]()
即![]()
所以![]()
化簡得: ![]() ,故
,故![]() 或
或![]() ,
,
結合![]() 知
知![]() ,
,
即直線![]() 恒過定點
恒過定點![]() .
.
(Ⅱ)由![]() 且
且![]() 得:
得: ![]() 或
或![]() ,
,
又![]()
![]()

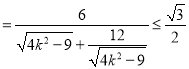 ,當且僅當
,當且僅當![]() ,即
,即![]() 時,
時, ![]() 的面積最大,最大值為
的面積最大,最大值為![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】一條光線從點(﹣2,﹣3)射出,經y軸反射后與圓(x+3)2+(y﹣2)2=1相切,則反射光線所在直線的斜率為( )
A.﹣![]() 或﹣
或﹣![]()
B.﹣![]() 或﹣
或﹣![]()
C.﹣![]() 或﹣
或﹣![]()
D.﹣![]() 或﹣
或﹣![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某手機賣場對市民進行國產手機認可度的調查,隨機抽取100名市民,按年齡(單位:歲)進行統計的頻數分布表和頻率分布直方圖如圖:
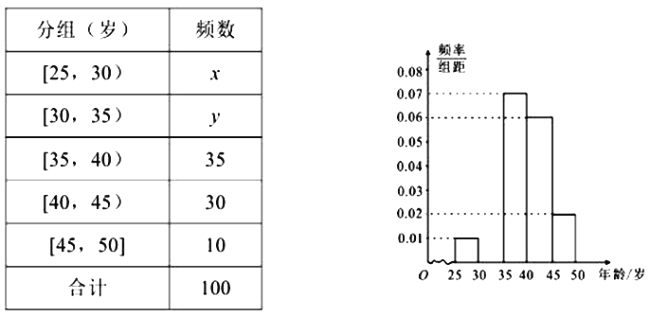
(Ⅰ)求頻率分布表中![]() ,
,![]() 的值,并補全頻率分布直方圖;
的值,并補全頻率分布直方圖;
(Ⅱ)在抽取的這100名市民中,按年齡進行分層抽樣,抽取20人參加國產手機用戶體驗問卷調查,現從這20人中隨機選取2人各贈送精美禮品一份,設這2名市民中年齡在![]() 內的人數
內的人數![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
以直角坐標系![]() 的原點為極點,
的原點為極點, ![]() 軸的非負半軸為極軸建立極坐標系,且兩坐標系有相同的長度單位.已知點
軸的非負半軸為極軸建立極坐標系,且兩坐標系有相同的長度單位.已知點![]() 的極坐標為
的極坐標為![]() ,
, ![]() 是曲線
是曲線![]() :
: ![]() 上任意一點,點
上任意一點,點![]() 滿足
滿足![]() ,設點
,設點![]() 的軌跡為曲線
的軌跡為曲線![]() .
.
(Ⅰ)求曲線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)若過點![]() 的直線
的直線![]() 的參數方程
的參數方程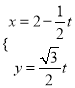 (
(![]() 為參數),且直線
為參數),且直線![]() 與曲線
與曲線![]() 交于
交于![]() ,
, ![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知直線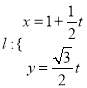 (
(![]() 為參數),曲線
為參數),曲線![]() (
(![]() 為參數).
為參數).
(1)設![]() 與
與![]() 相交于
相交于![]() 兩點,求
兩點,求![]() ;
;
(2)若把曲線![]() 上各點的橫坐標壓縮為原來的
上各點的橫坐標壓縮為原來的![]() 倍,縱坐標壓縮為原來的
倍,縱坐標壓縮為原來的![]() 倍,得到曲線
倍,得到曲線![]() ,設點
,設點![]() 是曲線
是曲線![]() 上的一個動點,求它到直線
上的一個動點,求它到直線![]() 的距離的最小值.
的距離的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知直線![]() 的極坐標方程為
的極坐標方程為![]() ),圓
),圓![]() 的參數方程為:
的參數方程為: ![]() (其中
(其中![]() 為參數).
為參數).
(1)判斷直線![]() 與圓
與圓![]() 的位置關系;
的位置關系;
(2)若橢圓的參數方程為 (
(![]() 為參數),過圓
為參數),過圓![]() 的圓心且與直線
的圓心且與直線![]() 垂直的直線
垂直的直線![]() 與橢圓相交于
與橢圓相交于![]() 兩點,求
兩點,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校從高二年級學生中隨機抽取60名學生,將其期中考試的政治成績(均為整數)分成六段: ![]() ,
, ![]() ,
, ![]() ,…
,…![]() 后得到如下頻率分布直方圖.
后得到如下頻率分布直方圖.
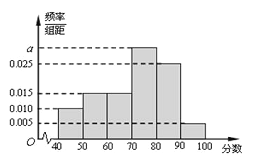
(1)根據頻率分布直方圖,估計該校高二年級學生期中考試政治成績的中位數(精確到0.1)、眾數、平均數;
(2)用分層抽樣的方法抽取一個容量為20的樣本,求各分數段抽取的人數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在幾何體ABDCE中,AB=AD,AE⊥平面ABD,M為線段BD的中點,MC∥AE,AE=MC.
(1)求證:平面BCD⊥平面CDE;
(2)若N為線段DE的中點,求證:平面AMN∥平面BEC.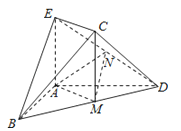
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示的是一個幾何體的直觀圖和三視圖(其中正視圖為直角梯形,俯視圖為正方形,側視圖為直角三角形).
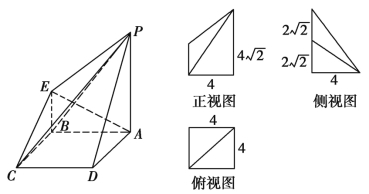
(1)求四棱錐P-ABCD的體積;
(2)若G為BC上的動點,求證:AE⊥PG.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com