
【題目】如圖,在四棱錐![]() 中,
中,![]() ,
,![]() ,平面
,平面![]() 平面PAD,E是
平面PAD,E是![]() 的中點,F是DC上一點,G是PC上一點,且
的中點,F是DC上一點,G是PC上一點,且![]() ,
,![]() .
.
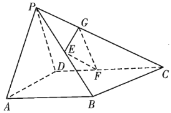
(1)求證:平面![]() 平面PAB;
平面PAB;
(2)若![]() ,
,![]() ,求直線PB與平面ABCD所成角的正弦值.
,求直線PB與平面ABCD所成角的正弦值.
【答案】(1)證明見解析;(2)![]()
【解析】
(1)從線面垂直的證明入手,證明![]() 平面PAB,從而證得平面
平面PAB,從而證得平面![]() 平面PAB;(2)添加輔助線,找到直線PB與平面ABCD所成的角,再在直角三角形中求其正弦值,也可以建立空間直角坐標系,利用空間向量法進行求解.
平面PAB;(2)添加輔助線,找到直線PB與平面ABCD所成的角,再在直角三角形中求其正弦值,也可以建立空間直角坐標系,利用空間向量法進行求解.
(1)如圖,取![]() 的中點M,連接MD,ME,
的中點M,連接MD,ME,
則![]() ,
,![]() .
.
又![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,
,
所以四邊形MDFE是平行四邊形,所以![]() .
.
因為![]() ,所以
,所以![]() .
.
因為平面![]() 平面PAD,平面
平面PAD,平面![]() 平面
平面![]() ,
,![]() ,所以
,所以![]() 平面PAD.
平面PAD.
因為![]() 平面PAD,所以
平面PAD,所以![]() .
.
因為![]() ,所以
,所以![]() 平面PAB,
平面PAB,
所以![]() 平面PAB.
平面PAB.
又![]() 平面EFG,所以平面
平面EFG,所以平面![]() 平面PAB.
平面PAB.

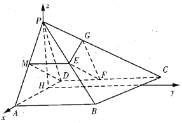
(2)解法—:過點P作![]() 于點H,則
于點H,則![]() 平面ABCD,以H為坐標原點,HA所在直線為x軸,過點H且平行于AB的直線為y軸,PH所在直線為z軸,建立如圖所示的空間直角坐標系
平面ABCD,以H為坐標原點,HA所在直線為x軸,過點H且平行于AB的直線為y軸,PH所在直線為z軸,建立如圖所示的空間直角坐標系![]() .
.
在等腰三角形PAD中,![]() ,
,![]() ,因為
,因為![]() ,所以
,所以![]() ,解得
,解得![]() ,則
,則![]() ,
,
所以 ,
,![]() ,所以
,所以 .
.
易知平面ABCD的一個法向量為![]() ,
,
所以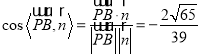 ,
,
所以直線PB與平面ABCD所成角的正弦值![]() .
.
解法二:由(1)可知![]() 平面PAD,
平面PAD,
因為![]() 平面PAD,所以
平面PAD,所以![]() .
.
在直角三角形PAB中,由勾股定理可得![]() .
.
過點P作![]() 于點H,則
于點H,則![]() 平面ABCD,連接HB,則
平面ABCD,連接HB,則![]() 是直線PB與平面ABCD所成的角.
是直線PB與平面ABCD所成的角.
在等腰三角形PAD中,![]() ,
,![]() ,
,
因為![]() ,所以
,所以![]() ,解得
,解得![]() ,在直角三角形PHB中,
,在直角三角形PHB中, .
.
所以直線PB與平面ABCD所成角的正弦值為![]() .
.


科目:高中數學 來源: 題型:
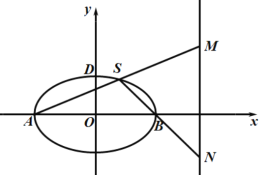
【題目】已知橢圓![]() 的左右頂點分別為A,B,離心率為
的左右頂點分別為A,B,離心率為![]() ,長軸長為4,動點S在C上位于x軸上方,直線
,長軸長為4,動點S在C上位于x軸上方,直線![]() 與直線
與直線![]() ,分別交于M,N兩點.
,分別交于M,N兩點.
(1)求橢圓C的方程
(2)求|MN|的最小值
(3)當![]() 最小時,在橢圓C上是否存在這樣的點T,使△TSB面積為
最小時,在橢圓C上是否存在這樣的點T,使△TSB面積為![]() ?若存在,請確定點T的個數;若不存在,請說明理由
?若存在,請確定點T的個數;若不存在,請說明理由
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,橢圓![]() 的右焦點、右頂點分別為F,A,過原點的直線與橢圓C交于點P、Q(點P在第一象限內),連結PA,QF.若
的右焦點、右頂點分別為F,A,過原點的直線與橢圓C交于點P、Q(點P在第一象限內),連結PA,QF.若![]() ,
,![]() 的面積是
的面積是![]() 面積的3倍.
面積的3倍.
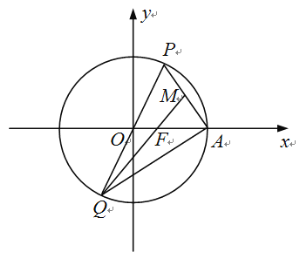
(1)求橢圓C的標準方程;
(2)已知M為線段PA的中點,連結QA,QM.
①求證:Q,F,M三點共線;
②記直線QP,QM,QA的斜率分別為![]() ,
,![]() ,
,![]() ,若
,若![]() ,求
,求![]() 的面積.
的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓![]() 的右焦點為
的右焦點為![]() ,以原點
,以原點![]() 為圓心,短半軸長為半徑的圓恰好經過橢圓
為圓心,短半軸長為半徑的圓恰好經過橢圓![]() 的兩焦點,且該圓截直線
的兩焦點,且該圓截直線![]() 所得的弦長為
所得的弦長為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)過定點![]() 的直線交橢圓
的直線交橢圓![]() 于兩點
于兩點![]() 、
、![]() ,橢圓上的點
,橢圓上的點![]() 滿足
滿足![]() ,試求
,試求![]() 的面積.
的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的一個焦點坐標為
的一個焦點坐標為![]() ,一條斜率為
,一條斜率為![]() 的直線分別交
的直線分別交![]() 軸于點
軸于點![]() ,交橢圓于點
,交橢圓于點![]() ,且點
,且點![]() 三等分
三等分![]() .
.
(1)求該橢圓的方程;
(2)若![]() 是第一象限內橢圓上的點,其橫坐標為2,過點
是第一象限內橢圓上的點,其橫坐標為2,過點![]() 的兩條不同的直線分別交橢圓于點
的兩條不同的直線分別交橢圓于點![]() ,且直線
,且直線![]() 的斜率之積
的斜率之積![]() ,求證:直線
,求證:直線![]() 恒過定點,并求出定點的坐標.
恒過定點,并求出定點的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年底,武漢發生了新冠肺炎疫情,2020年初開始蔓延.黨中央國務院面對“突發災難”果斷采取措施,舉國上下,萬眾一心支援武漢,全國各地醫療隊陸續增援湖北,紛紛投身疫情防控與救治病人之中.為了分擔“抗疫英雄”的后顧之憂,某校教師志愿者開展“愛心輔導”活動,為抗疫前線醫務工作者子女開展在線輔導.春節期間隨機安排甲乙兩位志愿者為一位初中生輔導功課共3次,每位志愿者至少輔導1次,每一次只有1位志愿者輔導,到甲恰好輔導兩次的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 的前
的前![]() 項和
項和![]() 滿足
滿足![]() (
(![]() ,
,![]() 為常數,
為常數,![]() ,且
,且![]() ),
),![]() ,
,![]() ,若存在正整數
,若存在正整數![]() ,使得
,使得![]() 成立;數列
成立;數列![]() 是首項為2,公差為
是首項為2,公差為![]() 的等差數列,
的等差數列,![]() 為其前
為其前![]() 項和,則以下結論正確的是( )
項和,則以下結論正確的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 滿足
滿足![]() .
.
(1)求數列![]() 的通項公式;
的通項公式;
(2)設![]() ,數列
,數列![]() 的前
的前![]() 項和為
項和為![]() ,求
,求![]() ;
;
(3)設![]() ,問:是否存在非零整數
,問:是否存在非零整數![]() ,使數列
,使數列![]() 為遞增數列?若存在,求出
為遞增數列?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)![]() x2+ax+lnx(a∈R)
x2+ax+lnx(a∈R)
(1)討論函數f(x)的單調性;
(2)若f(x)存在兩個極值點x1,x2且|x1﹣x2|![]() ,求|f(x1)﹣f(x2)|的最大值.
,求|f(x1)﹣f(x2)|的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com