
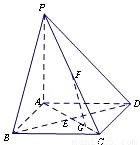
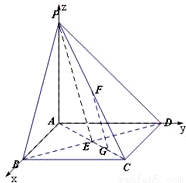
 如圖,在底面是正方形的四棱錐P-ABCD中,PA⊥面ABCD,BD交AC于點E,F是PC中點,G為AC上一點.
如圖,在底面是正方形的四棱錐P-ABCD中,PA⊥面ABCD,BD交AC于點E,F是PC中點,G為AC上一點.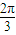 時,求PC與底面ABCD所成角的正切值.
時,求PC與底面ABCD所成角的正切值. 時,求PC與底面ABCD所成角的正切值.
時,求PC與底面ABCD所成角的正切值. AC時,FG∥平面PBD,(7分)
AC時,FG∥平面PBD,(7分)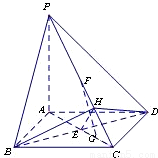 解(Ⅲ):作BH^PC于H,連接DH,
解(Ⅲ):作BH^PC于H,連接DH,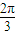 ,
,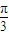 ,EH⊥PC,
,EH⊥PC,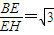 ,而BE=EC,
,而BE=EC,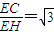 ,∴sinÐPCA=
,∴sinÐPCA=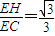 ,∴tanÐPCA=
,∴tanÐPCA=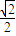 ,
,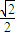 (14分)
(14分)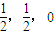 ),F(
),F(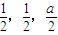 ),G(m,m,0)(0<m<
),G(m,m,0)(0<m< )(2分)
)(2分)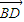 =(-1,1,0),
=(-1,1,0),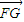 =(
=(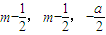 ),
),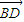 ×
×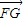 =-m+
=-m+ +m-
+m- +0=0,
+0=0,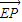 =(
=(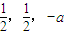 ),由
),由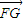 =l
=l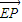 可得
可得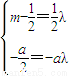 ,
,
 ,(7分)
,(7分) ,
, ,0),∴
,0),∴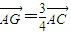 ,
, AC時,FG∥平面PBD(9分)
AC時,FG∥平面PBD(9分)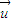 =(x,y,z),
=(x,y,z),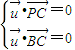 ,而
,而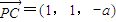 ,
,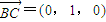 ,
,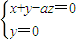 ,取z=1,得
,取z=1,得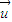 =(a,0,1),同理可得平面PDC的一個法向量為
=(a,0,1),同理可得平面PDC的一個法向量為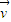 =(0,a,1),
=(0,a,1),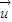 ,
,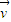 所成的角為q,則|cosq|=|cos
所成的角為q,則|cosq|=|cos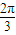 |=
|= ,即
,即 =
= ,∴
,∴ ,∴a=1(12分)
,∴a=1(12分) (14分)
(14分)

 新活力總動員暑系列答案
新活力總動員暑系列答案 龍人圖書快樂假期暑假作業鄭州大學出版社系列答案
龍人圖書快樂假期暑假作業鄭州大學出版社系列答案科目:高中數學 來源: 題型:
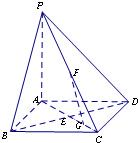 如圖,在底面是正方形的四棱錐P-ABCD中,PA⊥面ABCD,BD交AC于點E,F是PC中點,G為AC上一點.
如圖,在底面是正方形的四棱錐P-ABCD中,PA⊥面ABCD,BD交AC于點E,F是PC中點,G為AC上一點.查看答案和解析>>
科目:高中數學 來源: 題型:
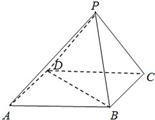 如圖,在底面是正方形的四棱錐P-ABCD中,平面PCD⊥平面ABCD,PC=PD=CD=2.
如圖,在底面是正方形的四棱錐P-ABCD中,平面PCD⊥平面ABCD,PC=PD=CD=2.查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,在底面是正方形的四棱錐P-ABCD中,PA⊥面ABCD,BD交AC于點E,F是PC中點,G為AC上一點.
如圖,在底面是正方形的四棱錐P-ABCD中,PA⊥面ABCD,BD交AC于點E,F是PC中點,G為AC上一點.| 2π | 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,在底面是正方形的四棱錐P-ABCD中,平面PCD⊥平面ABCD,PC=PD=CD=2.
如圖,在底面是正方形的四棱錐P-ABCD中,平面PCD⊥平面ABCD,PC=PD=CD=2.查看答案和解析>>
科目:高中數學 來源: 題型:
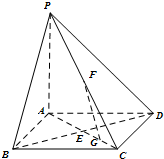 如圖,在底面是正方形的四棱錐P-ABCD中,PA⊥面ABCD,BD交AC于點E,F是PC中點,G為AC上一動點.
如圖,在底面是正方形的四棱錐P-ABCD中,PA⊥面ABCD,BD交AC于點E,F是PC中點,G為AC上一動點.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com