
【題目】設命題p:函數y=kx+1在R上是增函數,命題q:x∈R,x2+(2k﹣3)x+1=0,如果p∧q是假命題,p∨q是真命題,求k的取值范圍.
【答案】解:∵y=kx+1在R遞增,∴k>0,
由x∈R,x2+(2k﹣3)x+1=0,得方程x2+(2k﹣3)x+1=0有根,
∴△=(2k﹣3)2﹣4≥0,解得:k≤ ![]() 或k≥
或k≥ ![]() ,
,
∵p∧q是假命題,p∨q是真命題,
∴命題p,q一真一假,
①若p真q假,則 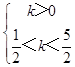 ,
,
∴ ![]() <k<
<k< ![]() ;
;
②若p假q真,則 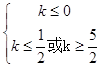 ,
,
∴k≤0;
綜上k的范圍是(﹣∞,0]∪( ![]() ,
, ![]() )
)
【解析】分別求出p,q為真時的k的范圍,根據p,q一真一假,得到關于k的不等式組,解出即可.
【考點精析】本題主要考查了復合命題的真假的相關知識點,需要掌握“或”、 “且”、 “非”的真值判斷:“非p”形式復合命題的真假與F的真假相反;“p且q”形式復合命題當P與q同為真時為真,其他情況時為假;“p或q”形式復合命題當p與q同為假時為假,其他情況時為真才能正確解答此題.


 小學教材全測系列答案
小學教材全測系列答案 小學數學口算題卡脫口而出系列答案
小學數學口算題卡脫口而出系列答案科目:高中數學 來源: 題型:
【題目】給出下列結論:
①y=x2+1,x∈[﹣1,2],y的值域[2,5]是;
②冪函數圖象一定不過第四象限;
③函數f(x)=loga(2x﹣1)﹣1的圖象過定點(1,0);
④若loga ![]() >1,則a的取值范圍是(
>1,則a的取值范圍是( ![]() ,1);
,1);
⑤函數f(x)= ![]() +
+ ![]() 是既奇又偶的函數;
是既奇又偶的函數;
其中正確的序號是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,正三棱柱ABC﹣A1B1C1的所有棱長都為2,D為CC1中點.試用空間向量知識解下列問題: 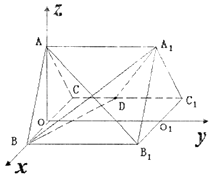
(1)求證:平面ABB1A1⊥平面A1BD;
(2)求二面角A﹣A1D﹣B的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() 的離心率為
的離心率為![]() ,且過點
,且過點![]() .若點
.若點![]() 在橢圓
在橢圓![]() 上,則點
上,則點![]() 稱為點
稱為點![]() 的一個“橢點”.
的一個“橢點”.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若直線![]() :
: ![]() 與橢圓
與橢圓![]() 相交于
相交于![]() ,
, ![]() 兩點,且
兩點,且![]() ,
, ![]() 兩點的“橢點”分別為
兩點的“橢點”分別為![]() ,
, ![]() ,以
,以![]() 為直徑的圓經過坐標原點,試求
為直徑的圓經過坐標原點,試求![]() 的面積.
的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知⊙C經過點A(﹣2,0),B(0,2),且圓心C在直線y=x上,直線L:y=kx+1與⊙C相交于P,Q點.
(1)求⊙C的方程.
(2)過點(0,1)作直線L1⊥L,且L1交⊙C于M,N,求四邊形PMQN的面積最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com