
【題目】已知命題![]() 函數
函數![]() 在
在![]() 上單調遞減;命題
上單調遞減;命題![]() 曲線
曲線![]() 為雙曲線.
為雙曲線.
(Ⅰ)若“![]() 且
且![]() ”為真命題,求實數
”為真命題,求實數![]() 的取值范圍;
的取值范圍;
(Ⅱ)若“![]() 或
或![]() ”為真命題,“
”為真命題,“![]() 且
且![]() ”為假命題,求實數
”為假命題,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1) ![]() (2)
(2) ![]()
【解析】
(I)對函數![]() 求導,利用分離常數法求得命題
求導,利用分離常數法求得命題![]() 中
中![]() 的取值范圍,利用雙曲線的標準方程的概念求得命題
的取值范圍,利用雙曲線的標準方程的概念求得命題![]() 中
中![]() 的取值范圍. 若“
的取值范圍. 若“![]() 且
且![]() ”為真命題則
”為真命題則![]() 均為真命題,求
均為真命題,求![]() 中兩個
中兩個![]() 的取值范圍的交集,得到題目所求
的取值范圍的交集,得到題目所求![]() 的取值范圍.(II)若“
的取值范圍.(II)若“![]() 或
或![]() ”為真命題,“
”為真命題,“![]() 且
且![]() ”為假命題,則
”為假命題,則![]() 一真一假,分別根據“
一真一假,分別根據“![]() 真
真![]() 假”或者“
假”或者“![]() 假
假![]() 真”兩類,結合(I)的數據,求得實數
真”兩類,結合(I)的數據,求得實數![]() 的取值范圍.
的取值范圍.
(Ⅰ)若![]() 為真命題,
為真命題,![]() 在
在![]() 恒成立,即
恒成立,即![]() 在
在![]() 恒成立,∵
恒成立,∵![]() 在
在![]() 的最大值是3,
的最大值是3,![]()
![]() ①
①
若![]() 為真命題,則
為真命題,則![]() ,解得
,解得![]() ,②
,②
若“![]() 且
且![]() ”為真命題,即
”為真命題,即![]() ,
,![]() 均為真命題,所以
均為真命題,所以![]() ,解得
,解得![]() ,
,
綜上所述,若“![]() 且
且![]() ”為真命題,則實數
”為真命題,則實數![]() 的取值范圍為
的取值范圍為![]() ;
;
(Ⅱ)若“![]() 或
或![]() ”為真命題,“
”為真命題,“![]() 且
且![]() ”為假命題,即
”為假命題,即![]() ,
,![]() 一真一假,
一真一假,
當![]() 真
真![]() 假時,
假時,![]() ,解得
,解得![]() ,
,
當![]() 假
假![]() 真時,
真時,![]() ,解得
,解得![]() ,
,
綜上所述,實數![]() 的取值范圍為
的取值范圍為![]() .
.


 直通貴州名校周測月考直通名校系列答案
直通貴州名校周測月考直通名校系列答案科目:高中數學 來源: 題型:
【題目】如圖,已知橢圓![]() :
:![]() 的離心率為
的離心率為![]() ,過左焦點
,過左焦點![]() 且斜率為
且斜率為![]() 的直線交橢圓
的直線交橢圓![]() 于
于![]() 兩點,線段
兩點,線段![]() 的中點為
的中點為![]() ,直線
,直線![]() :
:![]() 交橢圓
交橢圓![]() 于
于![]() 兩點.
兩點.

(1)求橢圓![]() 的方程;
的方程;
(2)求證:點![]() 在直線
在直線![]() 上;
上;
(3)是否存在實數![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值,若不存在,說明理由.
的值,若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某同學家門前有一筆直公路直通長城,星期天,他騎自行車勻速前往旅游,他先前進了![]() ,覺得有點累,就休息了一段時間,想想路途遙遠,有些泄氣,就沿原路返回騎了
,覺得有點累,就休息了一段時間,想想路途遙遠,有些泄氣,就沿原路返回騎了![]() , 當他記起詩句“不到長城非好漢”,便調轉車頭繼續前進. 則該同學離起點的距離
, 當他記起詩句“不到長城非好漢”,便調轉車頭繼續前進. 則該同學離起點的距離![]() 與時間
與時間![]() 的函數關系的圖象大致為( )
的函數關系的圖象大致為( )
A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知在四棱錐![]() 中,
中,![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,點
,點![]() 為棱
為棱![]() 的中點,
的中點,

(1)試在棱![]() 上確定一點
上確定一點![]() ,使平面
,使平面![]() 平面
平面![]() ,說明理由;
,說明理由;
(2)若![]() 為棱
為棱![]() 上一點,滿足
上一點,滿足![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為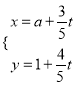 (
(![]() 為參數),在以
為參數),在以![]() 為極點,
為極點, ![]() 軸的正半軸為極軸的極坐標系中,曲線
軸的正半軸為極軸的極坐標系中,曲線![]() 的方程為
的方程為![]() .
.
(1)求直線![]() 和曲線
和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)已知點![]() ,設直線
,設直線![]() 與曲線
與曲線![]() 的兩個交點為
的兩個交點為![]() ,
, ![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 和圓
和圓![]() ,過
,過![]() 的動直線
的動直線![]() 與圓
與圓![]() 交于
交于![]() 、
、![]() 兩點,過
兩點,過![]() 作直線
作直線![]() ,交
,交![]() 于
于![]() 點.
點.

(Ⅰ)求動點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(Ⅱ)若不經過![]() 的直線
的直線![]() 與軌跡
與軌跡![]() 交于
交于![]() 兩點,且
兩點,且![]() .求證:直線
.求證:直線![]() 恒過定點.
恒過定點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義在![]() 上的偶函數
上的偶函數![]() 和奇函數
和奇函數![]() ,且
,且![]() .
.
(1)求函數![]() ,
,![]() 的解析式;
的解析式;
(2)設函數 ,記
,記![]()
![]() .探究是否存在正整數
.探究是否存在正整數![]() ,使得對任意的
,使得對任意的![]() ,不等式
,不等式![]() 恒成立?若存在,求出所有滿足條件的正整數
恒成立?若存在,求出所有滿足條件的正整數![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com