
【題目】已知點P(2,0),且圓C:x2+y2﹣6x+4y+4=0.
(Ⅰ)當直線![]() 過點P且與圓心C的距離為1時,求直線
過點P且與圓心C的距離為1時,求直線![]() 的方程;
的方程;
(Ⅱ)設過點P的直線與圓C交于A、B兩點,若|AB|=4,求以線段AB為直徑的圓的方程.
【答案】(1)x=2;(2)(x-2)2+y2=4
【解析】本試題主要是考查了直線與圓的位置關系的運用。以及圓的方程的求解問題。
(1)因為設直線l的斜率為k(k存在)則方程為y-0=k(x-2)
又⊙C的圓心為(3,-2) ,r=3,利用線與圓的位置關系可知直線的方程。
(2)根據設過點P的直線與圓C交于A、B兩點,當|AB|=4,利用半徑長和半弦長,弦心距的勾股定理得到結論。
解:(1)設直線l的斜率為k(k存在)則方程為y-0=k(x-2) …………………1分
又⊙C的圓心為(3,-2) ,r=3
由![]() ……………………4分
……………………4分
所以直線方程為![]() ……………………6分
……………………6分
當k不存在時,l的方程為x=2. ……………………8分
(2)由弦心距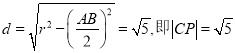 , ……………………11分
, ……………………11分
知P為AB的中點,故以AB為直徑的圓的方程為(x-2)2+y2=4. …………………14分


 53天天練系列答案
53天天練系列答案科目:高中數學 來源: 題型:
【題目】某商場銷售某種品牌的空調器,每周周初購進一定數量的空調器,商場沒銷售一臺空調器可獲利500元,若供大于求,則每臺多余的空調器需交保管費100元;若供不應求,則可從其他商店調劑供應,此時每臺空調器僅獲利潤200元.
(Ⅰ)若該商場周初購進20臺空調器,求當周的利潤(單位:元)關于當周需求量![]() (單位:臺,
(單位:臺,![]() )的函數解析式
)的函數解析式![]() ;
;
(Ⅱ)該商場記錄了去年夏天(共10周)空調器需求量(單位:臺),整理得下表:

以10周記錄的各需求量的頻率作為各需求量發生的概率,若商場周初購進20臺空調器,![]() 表示當周的利潤(單位:元),求
表示當周的利潤(單位:元),求![]() 的分布及數學期望.
的分布及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“奶茶妹妹”對某時間段的奶茶銷售量及其價格進行調查,統計出售價![]() 元和銷售量
元和銷售量![]() 杯之間的一組數據如下表所示:
杯之間的一組數據如下表所示:
價格 | 5 | 5.5 | 6.5 | 7 |
銷售量 | 12 | 10 | 6 | 4 |
通過分析,發現銷售量![]() 對奶茶的價格
對奶茶的價格![]() 具有線性相關關系.
具有線性相關關系.
(Ⅰ)求銷售量![]() 對奶茶的價格
對奶茶的價格![]() 的回歸直線方程;
的回歸直線方程;
(Ⅱ)欲使銷售量為![]() 杯,則價格應定為多少?
杯,則價格應定為多少?
附:線性回歸方程為![]() ,其中
,其中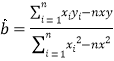 ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,等邊三角形ABC的邊長為4,M,N分別為AB,AC的中點,沿MN將△AMN折起,使點A到A′的位置.若平面A′MN與平面MNCB垂直,則四棱錐A′MNCB的體積為________.
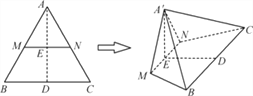
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() 為自然對數的底數),
為自然對數的底數),![]()
![]() ,
,![]() .
.
(1)求曲線![]() 在
在![]() 處的切線方程;
處的切線方程;
(2)討論函數![]() 的極小值;
的極小值;
(3)若對任意的![]() ,總存在
,總存在![]() ,使得
,使得![]() 成立,求實數
成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知:以點![]() (
(![]() )為圓心的圓與
)為圓心的圓與![]() 軸交
軸交
于點O, A,與y軸交于點O, B,其中O為原點.
(1)求證:△OAB的面積為定值;
(2)設直線![]() 與圓C交于點M, N,若OM = ON,求圓C的方程.
與圓C交于點M, N,若OM = ON,求圓C的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某商店計劃每天購進某商品若干件,商店每銷售1件該商品可獲利50元.若供大于求,剩余商品全部退回,則每件商品虧損10元;若供不應求,則從外部調劑,此時每件調劑商品可獲利30元.
(Ⅰ)若商店一天購進該商品10件,求當天的利潤y(單位:元)關于當天需求量n(單位:件,n∈N)的函數解析式;
(Ⅱ)商店記錄了50天該商品的日需求量(單位:件),整理得下表:
日需求量n | 8 | 9 | 10 | 11 | 12 |
頻數 | 10 | 10 | 15 | 10 | 5 |
①假設該店在這50天內每天購進10件該商品,求這50天的日利潤(單位:元)的平均數;
②若該店一天購進10件該商品,記“當天的利潤在區間![]() ”為事件A,求P(A)的估計值.
”為事件A,求P(A)的估計值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點A(1,a),圓x2+y2=4.
(1)若過點A的圓的切線只有一條,求a的值及切線方程;
(2)若過點A且在兩坐標軸上截距相等的直線被圓截得的弦長為![]() ,求a的值.
,求a的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com