
【題目】如圖,直角梯形![]() 與等腰直角三角形
與等腰直角三角形![]() 所在的平面互相垂直,
所在的平面互相垂直,![]() .
.

(1)求直線![]() 與平面
與平面![]() 所成角的正弦值;
所成角的正弦值;
(2)線段![]() 上是否存在點
上是否存在點![]() ,使
,使![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() ;若不存在,說明理由.
;若不存在,說明理由.
【答案】(1)![]() ;(2)點
;(2)點![]() 滿足
滿足![]() 時,有
時,有![]() .
.
【解析】
試題分析:(1)先證明![]() 兩兩垂直,通過建立適當(dāng)?shù)淖鴺?biāo)系,向量法求解;(2)通過線
兩兩垂直,通過建立適當(dāng)?shù)淖鴺?biāo)系,向量法求解;(2)通過線![]() 的方向向量和平面
的方向向量和平面![]() 的法向量垂直證明
的法向量垂直證明![]() .
.
試題解析:![]() 取
取![]() 的中點
的中點![]() ,連
,連![]() ,則
,則![]() ,因為平面
,因為平面![]() ,且
,且![]() ,平面
,平面![]() ,所以
,所以![]() ,所以
,所以![]() ,由
,由![]() 兩兩垂直,建立如圖所示的空間直角坐標(biāo)系
兩兩垂直,建立如圖所示的空間直角坐標(biāo)系![]() .
.

因為三角形![]() 為等腰直角三角形,所以
為等腰直角三角形,所以![]() ,設(shè)
,設(shè)![]() ,
,
所以![]() ,所以
,所以![]() ,平面
,平面![]() 的一個法向量為
的一個法向量為![]() .設(shè)直線
.設(shè)直線![]() 與平面
與平面![]() 所成角為
所成角為![]()
![]() ,所以
,所以 .即直線
.即直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() .
.
![]() 存在點
存在點![]() ,且
,且![]() 時, 有
時, 有![]() .證明如下:假設(shè)
.證明如下:假設(shè)![]() 上存在點
上存在點![]() ,使得
,使得![]()
平面![]() ,
,

連接![]() 交
交![]() 于點
于點![]() ,連接
,連接![]() ,則
,則![]() ,所以
,所以![]() , 由
, 由![]() ,得
,得![]() ,
,
其他證明方法:由![]()
![]() ,所以
,所以![]() ,設(shè)平面
,設(shè)平面![]() 的一個法向量為
的一個法向量為![]() ,則有
,則有 ,所以
,所以 ,取
,取![]() 得,
得,![]() ,
,
因為![]() ,且
,且![]() ,所以
,所以![]() .即點
.即點![]() 滿足
滿足![]() 時,有
時,有![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】 等差數(shù)列{an}中,a1=-5,它的前11項的平均值是5,若從中抽取1項,余下10項的平均值是4,則抽取的是第 項.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某制造廠商10月份生產(chǎn)了一批乒乓球,從中隨機抽取![]() 個進(jìn)行檢查,測得每個球的直徑(單位:
個進(jìn)行檢查,測得每個球的直徑(單位:![]() ),將數(shù)據(jù)進(jìn)行分組,得到如下頻率分布表:
),將數(shù)據(jù)進(jìn)行分組,得到如下頻率分布表:
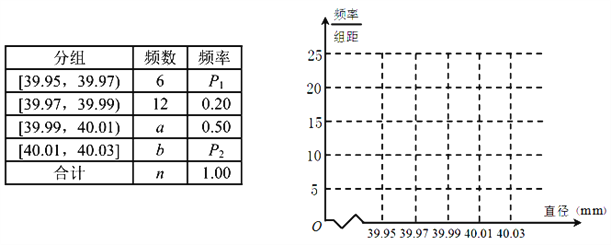
(1)求![]() 、
、![]() 、
、![]() 及
及![]() 、
、![]() 的值,并畫出頻率分布直方圖(結(jié)果保留兩位小數(shù));
的值,并畫出頻率分布直方圖(結(jié)果保留兩位小數(shù));
(2)已知標(biāo)準(zhǔn)乒乓球的直徑為![]() ,且稱直徑在
,且稱直徑在![]() 內(nèi)的乒乓球為五星乒乓球,若這批乒乓球共有
內(nèi)的乒乓球為五星乒乓球,若這批乒乓球共有![]() 個,試估計其中五星乒乓球的數(shù)目;
個,試估計其中五星乒乓球的數(shù)目;
(3)統(tǒng)計方法中,同一組數(shù)據(jù)常用該組區(qū)間的中點值(例如區(qū)間![]() 的中點值是
的中點值是![]() )作為代表,試估計這批乒乓球直徑的平均值和中位數(shù).
)作為代表,試估計這批乒乓球直徑的平均值和中位數(shù).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
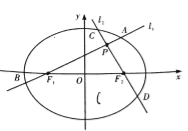
【題目】如圖,分別過橢圓![]() 左、右焦點
左、右焦點![]() 的動直線
的動直線![]() 相交于
相交于![]() 點,與橢圓
點,與橢圓![]() 分別交于
分別交于![]() 與
與![]() 不同四點,直線
不同四點,直線![]() 的斜率
的斜率![]() 滿足
滿足![]() , 已知
, 已知![]() 與
與![]() 軸重合時,
軸重合時, ![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)是否存在定點![]() 使得
使得![]() 為定值,若存在,求出
為定值,若存在,求出![]() 點坐標(biāo)并求出此定值,若不存在,
點坐標(biāo)并求出此定值,若不存在,
說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】函數(shù)f(x)=log3(2﹣x)的定義域是( )
A.[2,+∞)B.(2,+∞)C.(﹣∞,2)D.(﹣∞,2]
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知實數(shù)![]() ,函數(shù)
,函數(shù)![]() .
.
(1)當(dāng)![]() 時,求
時,求![]() 的最小值;
的最小值;
(2)當(dāng)![]() 時,判斷
時,判斷![]() 的單調(diào)性,并說明理由;
的單調(diào)性,并說明理由;
(3)求實數(shù)![]() 的范圍,使得對于區(qū)間
的范圍,使得對于區(qū)間 上的任意三個實數(shù)
上的任意三個實數(shù)![]() ,都存在以
,都存在以![]() 為邊長的三角形.
為邊長的三角形.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】對于數(shù)列![]() ,
,![]() ,
,![]() 為數(shù)列
為數(shù)列![]() 是前
是前![]() 項和,且
項和,且![]() ,
,![]() ,
,![]() .
.
(1)求數(shù)列![]() ,
,![]() 的通項公式;
的通項公式;
(2)令![]() ,求數(shù)列
,求數(shù)列![]() 的前
的前![]() 項和
項和![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某大學(xué)生在開學(xué)季準(zhǔn)備銷售一種文具盒進(jìn)行試創(chuàng)業(yè),在一個開學(xué)季內(nèi),每售出1盒該產(chǎn)品獲利潤50元,未售出的產(chǎn)品,每盒虧損30元.根據(jù)歷史資料,得到開學(xué)季市場需求量的頻率分布直方圖,如圖所示.該同學(xué)為這個開學(xué)季購進(jìn)了160盒該產(chǎn)品,以![]() (單位:盒,
(單位:盒,![]() )表示這個開學(xué)季內(nèi)的市場需求量,
)表示這個開學(xué)季內(nèi)的市場需求量,![]() (單位:元)表示這個開學(xué)季內(nèi)經(jīng)銷該產(chǎn)品的利潤.
(單位:元)表示這個開學(xué)季內(nèi)經(jīng)銷該產(chǎn)品的利潤.
(1)根據(jù)直方圖估計這個開學(xué)季內(nèi)市場需求量![]() 和中位數(shù);
和中位數(shù);
(2)將![]() 表示為
表示為![]() 的函數(shù);
的函數(shù);
(3)根據(jù)直方圖估計利潤![]() 不少于4800元的概率
不少于4800元的概率
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com